Задать вопрос Регистрация
Помочь другим

  • Составить уравнение нормали и касательной к кривой y = [tex] \frac{4x- x^{2} }{4} [/tex] в точке с абсциссой [tex] x_{0} [/tex] = 2

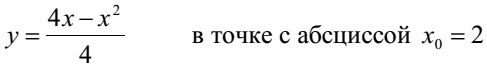
    question img

Ответы 2

  • Спасибо большое!

  • y=\frac{4x-x^2}{4}\; ,\; \; x_0=2\\\\y(2)=\frac{8-4}{4}=1\\\\y'=(x-\frac{x^2}{4})'=1-\frac{x}{2}\; ,\; \; y'(2)=1-1=0\\\\kasatelnaya:\; \; y=y(x_0)+y'(x_0)\cdot (x-x_0)\\\\y=1+0\cdot (x-2)\\\\\underline {y=1}\\\ormal:\; \; \underline {x=2}

    Нормаль перпендикулярна касательной. В точке с абсциссой х=2 находится вершина параболы y=x-\frac{x^2}{4} . Поэтому прямая х=2 будет нормалью к касательной у=1.

    • Автор:

      daugherty
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years