Задать вопрос Регистрация
Помочь другим

  • помогите решить диф. уравнение. даю 20 баллов. нужно второе

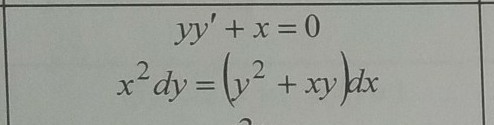
    question img

Ответы 1

  • Это уравнение можно переписать как x^2y'=y^2+xy - однородное уравнение, так как выполняется условие однородности.

    Пусть y=ux , тогда дифференцируя(по формуле дифференцирования произведения двух функций):

    y'=u'x+u и подставим в уравнение

    x^2(u'x+u)=u^2x^2+ux^2\\ u'x+u=u^2+u\\ u'x=u^2

    Получили уравнение с разделяющимися переменными:

    \displaystyle \int \frac{du}{u^2} =\int\frac{dx}{x} ~~\Rightarrow~~-\frac{1}{u} =\ln |x|+C

    Обратная замена:

    -\dfrac{x}{y} =\ln |x|+C - ОБЩИЙ ИНТЕГРАЛ

    • Автор:

      bugsythm5
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years