-
помогите плиззз..............
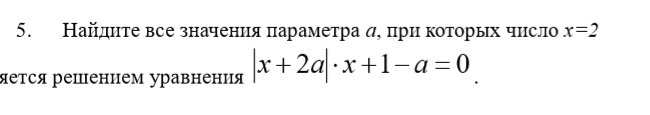
-
Предмет:
Математика -
Автор:
yolanda - 6 лет назад
-
Ответы 1
-
Подставим корень
в заданное уравнение:
Уравнение имеет решение, если правая часть уравнения неотрицательно.
При
откуда
возводим в квадрат левую и правую части уравнения.
Найдем корни не удовлетворяют нашем условию
, следовательно, таких параметров а нет.
Ответ: таких параметров а - нет.
-
Автор:
alex7 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найдите значение выражения ctg(31π−7π/4)
-
Предмет:
Математика -
Автор:
wilma - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
2^x+2^2-х=5 спасите помогите
-
Предмет:
Математика -
Автор:
gigglesohhb - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Хороша верёвка длинная, а речь короткая. Не торопись отвечать, торопись изучать. Мягко стелет, да жёстко падает. Где тонко там и -? Худой мир лучше доброй -? Сам кашу заварил, сам и еш. Что посеешь, то и по жмёш. Дерево ценят по плодам, а человека словам?(не уверена) Лучше хорошо поступать, чем хорошо -? Прощай другим, но не прощай -? Молодец против овец, а против молодца и с-?
Надо дописать пословицы кое какие написала но не уверена
-
Предмет:
Русский язык -
Автор:
cecilian7ms - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сколько натуральных чисел, меньших 200, которые делятся на 5 и на 6, но не делятся на 60?
-
Предмет:
Математика -
Автор:
kaylensolomon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
