Задать вопрос Регистрация
Помочь другим

  • Найти корень уравнения 2*cos(x)^2+3*sin(x-pi/2)-2 =0 принадлежащий промежутку [-pi; pi/2].

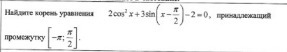
    question img

Ответы 3

  • решение исправил

    • Автор:

      violet87
    • 5 лет назад
    • 0
  • спасибо огромное..я как раз и решил до момента с arccos'инусами

    • Автор:

      sincere
    • 5 лет назад
    • 0

  • 2\cos^2x+3\sin(x-\frac{\pi}{2})-2=0\\ 2\cos^2x-3\cos x-2=0

    Решим это уравнение как квадратное уравнение относительно cos x:

    D=b^2-4ac=(-3)^2-4\cdot 2\cdot (-2)=9+16=25

    \cos x=\frac{3+5}{2\cdot 2} =2 - уравнение решений не имеет, так как косинус принимает свои значения [-1;1].

    \cos x=\frac{3-5}{2\cdot 2} =-0.5~~\Rightarrow~~ x=\pm\frac{2\pi}{3} +2\pi n,n \in \mathbb{Z}

    Корней на промежутке [-\pi ;\frac{\pi}{2}] : - \frac{2 \pi }{3} .

    • Автор:

      molina33
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years