-
Надо найти точку, в которой функция принимает наименьшее значение на отрезке [10;12]
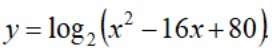
-
Предмет:
Математика -
Автор:
chaz95 - 6 лет назад
-
Ответы 2
-
y=log₂(x²-16x+80)
Найдем первую производную и приравняем к 0, чтобы найти точки max и min:
y'=(log₂(x²-16x+80))'=
=(2x-16)/(ln2•(x²-16x+80))=0
Тогда 2x-16=0 <=> x=8
Находим вторую производную:
y''=(-2x²+32x-96)/(ln2•(x²-16x+80)²)=
=(-2•8²+32•8-96)/(ln2•(8²-16•8+80)²)=
=1/(8ln2)>0, значит x=8 - точка min.
Значит на промежутке [10;12] функция будет возрастать, а следовательно наименьшее значение функция будет иметь в точке x=10, тогда:
y=log₂(x²-16x+80)=
=log₂(10²-16•10+80)=2+log₂5
Ответ: (10;2+log₂5).
-
Автор:
smoochie - 6 лет назад
-
0
-
-
У подлогарифмического дискриминант отрицательный, значит оно никогда не обращается в 0
Наименьшее его значение в минимуме
-b/2a=16/2=8
Получается до 8 убывает, после 8 возрастает
У нас ограничение от 10 до 12
Значит 10 наименьшее

-
Автор:
bella5 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
1)6,965+23,3
2)88,000-9,804
3)16,94:2,8
4)5_6+1_4 (пять шестых + одна четвертая)
5)3_10-4_15 (три десятых - четыре пятнадцатых)
6)4_9x4_9 (четыре девятых умножить на четыре девятых)
7)Найти 25% от чисел:
а)200
б)3
в)5,7-
Предмет:
Математика -
Автор:
calimalone - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Спишите вставьте пропущенные буквы Выделите окончания прилагательных выполнить синтаксический разбор выделенных предложений
1.Тихо стараясь обмануть хищников кр..дется заяц по мягк.. снегу(4).
В Нов... Зеланд... об...тают два типа летуч... мышей. Лес теперь был похож... на могуч... льва.Он прихрамывал на задн... лапу. Побелел син... снег. Задремавшая река отр...жает обл..ка, тих.., бледн... свод небес ,тих..., темн...., сонн... лес(4).
С моря слышен смутн... гул. Со..нце пахнет травами . свеж.. купавами, пробужденною весной и смолистою сосной(4). Лосенок был мал...ньк.. , ж..лт..ньк... , с больш... , как у осла ушами. Птица одна за другой больш.. кругами поднималась над горн.. хре...том навстречу утренн... ветру. Отара овец пасущаяся на склон... горы пох...дила на весенн.... курчав.. обл...ч..ко(4)
2.выполните морфологический разбор
стараясь, тихо, мягкому, обитают , два , теперь , хорош, на льва, прихрамывал, задремавшая , с моря , навстречу(ветру), утреннему, пасущаяся (см.задание 1)-
Предмет:
Русский язык -
Автор:
everett57 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Главные герои рассказа маленький принц!!!!!
Помогите СРОЧНО!!!!!-
Предмет:
Литература -
Автор:
joanoliver - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите ПЖ очень надо
Знайти суму 5 перших членів арифметичной прогрессии 3, -2. -7
