-
Задача номер 1
Найдите х из рисунка- номер 4
Ответ: 26°
Задача номер 2
Градусная мера дуги АВ равна 60°. Найдите длину диаметр окружности, если известно, что длина хорды АВ равна8 см.
Ответ: 16
Задача номер 3
Две окружности, радиусом 10 см и 15см пересекаются. Найдите наибольшее целое значение, которое может принимать расстояние между центрами окружностей
Ответ: 24 см.
Помогите пожалуйста.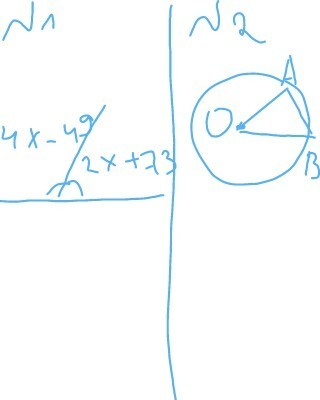
-
Предмет:
Математика -
Автор:
mayzg2p - 6 лет назад
-
Ответы 1
-
1.
(4х - 49°) + (2х + 73°) = 180°,
4х + 2х = 180° + 49° - 73°,
6х = 156°,
х = 26°,
4х - 49° = 55° - угол 1,
2х + 73° = 125° - угол 2,
2.
так как ОА и ОВ - радиусы, то ОА = ОА, а ΔОАВ - равнобедреный, поэтому:
∠А = ∠В = (180° - 60°) / 2 = 60°,
из данного расчета видно, что ΔОАВ - равносторонний, значит:
ОА = ОВ = АВ = 8 см, следовательно:
диаметр окружности равен:
d = 2r = 2*ОА = 2 * 8 = 16 см,
3.
если окружности соприкосаются, то расстояние между их центрами будет равно:
10 + 15 = 25 см,
если данные окружности пересекаются, то наибольшим расстоянием между их центрами будет целое число:
25 - 1 = 24 см
-
Автор:
tyson40 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Очень краткое содержание "Одиссей у Циклопа" ОЧЕНЬ СРОЧНО!!!!
-
Предмет:
Литература -
Автор:
big nastygcxk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите все натуральные значения в,при которых дробь 4b+1/17 будет правильной
-
Предмет:
Математика -
Автор:
sierrahatfield - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Можно пожалуйста очень краткое содержание книги Майская ночь или утопленница
-
Предмет:
Литература -
Автор:
nicanors3m7 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Позначити рядок, у якому вжито прийменник:
А. Ще й треті півні не співали.
Б. Швидше на долоні волосся виросте.
В. Хоч ікону малюй.
Г. Не було й гадки.-
Предмет:
Українська мова -
Автор:
dereon - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
