-
Найдите все положительные значения a, при каждом из которых система имеет единственное решение
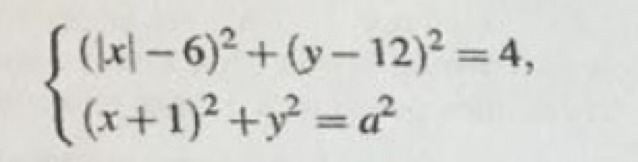
-
Предмет:
Математика -
Автор:
gordo3fbp - 6 лет назад
-
Ответы 2
-
1-е уравнение задаёт 2 окружности радиуса 2. Центры -
и
2-е уравнение задаёт окружность радиуса
(но в нашей задаче просто a, так как по условию a>0). Центр -
Решаем графически, когда есть 1 решение:
Красным на рисунке 1-е уравнение, синим - 2-е.
1-е решение будет касание левой окружности (т.к. она ближе к точке M)
Опускаем перпендикуляр как на рисунке и по т. Пифагора:
2-е решение (единственное) будет при касании правой красной окружности синей внутренним образом.
Опускаем перпендикуляр как на рисунке и по т. Пифагора:
Ответ:

-
Автор:
ceceliaqxtb - 6 лет назад
-
0
-
-
Решение во вложении.

-
Автор:
alejandrotasf - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как решать деление дробей с разными знаменателями?
-
Предмет:
Математика -
Автор:
peck - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Обчислите суму бесконечной геометрической прогресиии 1 член = 14,а знаменатель одна вторая найти S=в1
-
Предмет:
Математика -
Автор:
raidenreilly - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ученикам 7 класса ВОПРОС
Каким оружием обладали марсиане
в книге Герберта Уэллса «Война миров»?-
Предмет:
Литература -
Автор:
quintinx4x9 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
решить систему уровнений
{4x+9y=5
{2x-y=-3-
Предмет:
Математика -
Автор:
maryqeud - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
