-
Помогите, пожалуйста, упростить выражения с объяснением 144-148!!!!
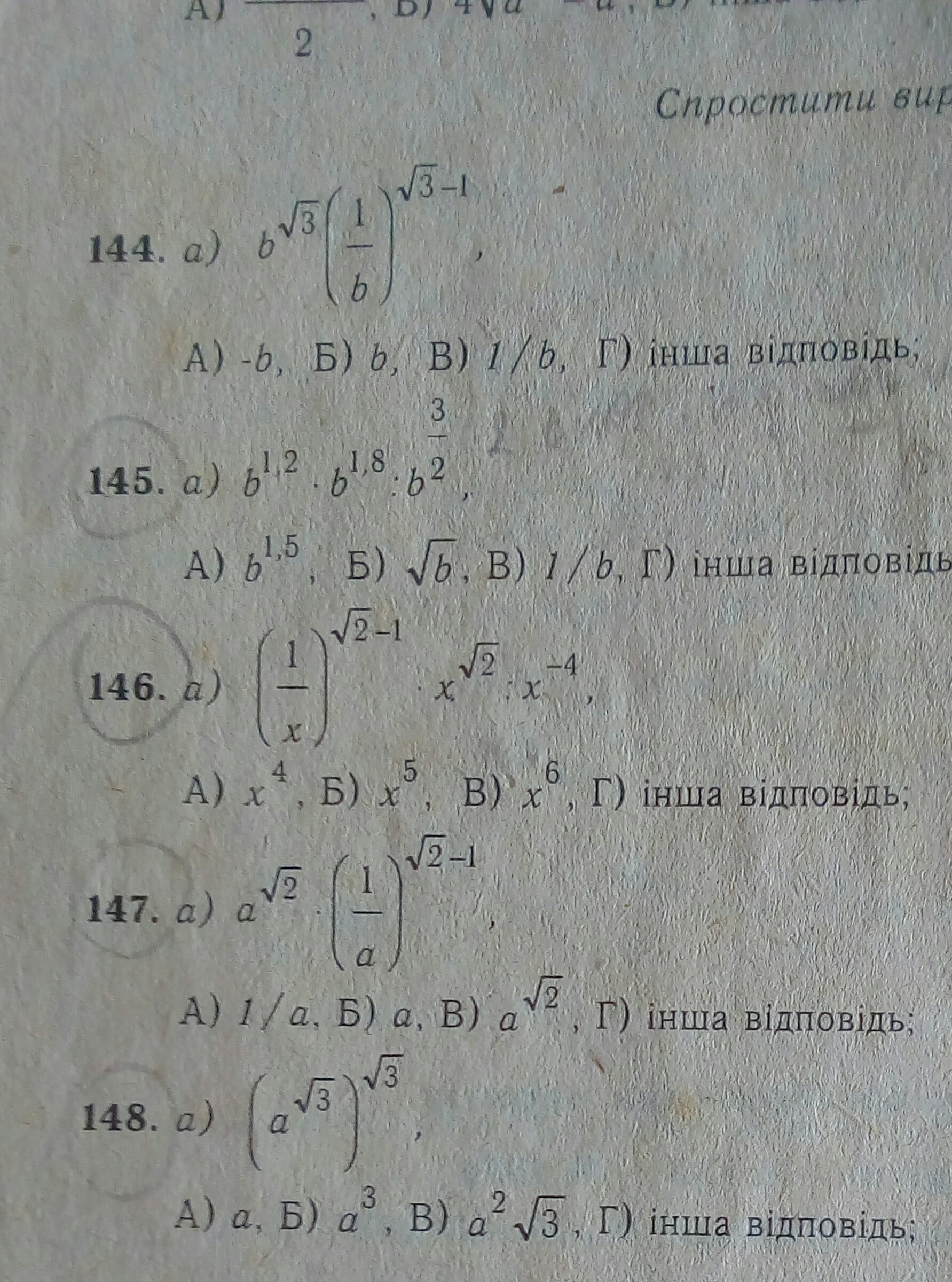
-
Предмет:
Математика -
Автор:
chiquitaatk6 - 6 лет назад
-
Ответы 4
-
ваш текст не отображается!
-
Автор:
clarkkemp - 6 лет назад
-
0
-
-
нужно вставить
-
Автор:
shaun - 6 лет назад
-
0
-
-
Формулы со степенями на картинке

-
Автор:
daniel10 - 6 лет назад
-
0
-
-
144) b^{\sqrt{3}}*(\frac{1}{b})^{\sqrt{3}-1}=b^{\sqrt{3}}*b^{1-\sqrt{3}}=b^{\sqrt{3}+1-\sqrt{3}}=b\\\\145) b^{1,2}*b^{1,8}:b^{\frac{3{2}}=b^{1,2}*b^{1,8}:b^{1,5}=b^{1,2+1,8-1,5}=b^{1,5}\\\\146) (\frac{1}{x})^{\sqrt{2}-1}*x^{\sqrt{2}}:x^{-4}=x^{1-\sqrt{2}}*x^{\sqrt{2}}:x^{-4}=x^{1-\sqrt{2}+\sqrt{2}+4}=x^{5}\\\\147) a^{\sqrt{2}} *(\frac{1}{a})^{\sqrt{2}-1} =a^{\sqrt{2}}*a^{1-\sqrt{2}}=a^{\sqrt{2}+1-\sqrt{2}}=a\\\\148) (a^{\sqrt{3}})^{\sqrt{3}}

-
Автор:
lee66 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Функции
В) Постройте график функции y=-45x, выбрав масштаб: по оси x - в одной клетке - одна единица, по оси y - в одной клетке - десять единиц.
Умоляю Прошу СРОЧНО ну
жно даю 10 баллов-
Предмет:
Алгебра -
Автор:
jimenagoei - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Даны точки A(1;1), B(-1;0), C(0;1). Найти такую точку K(x;y), чтобы векторы AB и CK были равны.
-
Предмет:
Математика -
Автор:
kylie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- При взаємодії 34.24 г двовалентного металу з водою виділився водень масою 0,5г.Визначте метал.
-
В правильной четырехугольной пирамиде плоский угол равен a. Чему равен двухгранный угол x при основании?
A) cosx = tga
B) cosx = ctga
C) cosx = tg(a/2)
D) cosx = ctg(a/2)
Если не затруднит, дайте определение плоского и двухгранного угла, или изобразите на рисунке, если возможно. Заранее спасибо)-
Предмет:
Математика -
Автор:
sue - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
