-
СРОЧНО! ПОМОГИТЕ! БУДУ ОЧЕНЬ БЛАГОДАРНА! Помогите решить уравнения , все 3
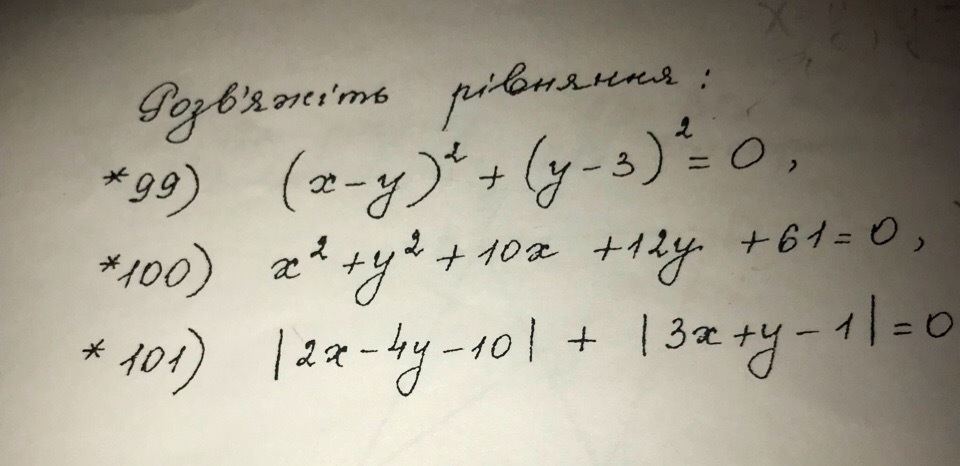
-
Предмет:
Математика -
Автор:
amorcita - 6 лет назад
-
Ответы 1
-
99)(х-у)²+(у-3)²=0Т.к. квадраты (х-у)²≥0 и (у-3)²≥0, то равенство их суммы будет достигаться при равенстве каждого из слагаемых нулюпоэтому имеем х-у=0 и у-3=0откуда х=3, у=3100)х²+у²+10х+12у+61=0х²+10х+25+ у²+12у+36=0(х+5)²+(у+6)²=0аналогично рассуждая, получим равенство нулю каждого из слагаемыхоткуда х+5=0 у+6=0х= -5 у= -6101)|2х-4у-10|+|3х+у-1|=0значение любого модуля всегда ≥0поэтому равенство суммы двух модулей будет достигаться при равенстве каждого из этих модулей нулю.а модуль будет равен нулю, когда подмодульное выражение равно нулю.Получаем систему:2х-4у-10=03х+у-1=0или х-2у=53х+у=1(решаем построением, см чертеж)решением системы будут :х=1 у= -2

-
Автор:
santiago989 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найти значение выражения -12,3+8,5-1,9
-
Предмет:
Математика -
Автор:
raven84 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В чем смысл рассказа " Жалобная книга "- Чехов .
-
Предмет:
Литература -
Автор:
aishasn6x - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите пожалуйста решить задачу. от прямоугольного листа со сторонами 5 см и 3 см отрезали полоску со сторонами 3 см и 1 см. найди площадь оставшейся части?
-
Предмет:
Математика -
Автор:
sarax4lk - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Какое android-приложение посоветуете для заучивания дат по истории?
How much to ban the user?
1 hour
1 day
100 years
