-
Помогите пожалуйста.
Математика. Автор: с.г.григорьев и задулина
Тема: Функция одной переменной
Предел функции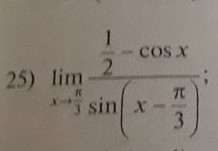
-
Предмет:
Математика -
Автор:
cindyduran - 6 лет назад
-
Ответы 4
-
Интересно,но такого правила мы ещё не знаем,ну или только я не знаю)))
-
Автор:
dalton13 - 6 лет назад
-
0
-
-
Ну, скорее всего значит там можно как-то преобразовать выражение под пределом. Котелок пока не доварил.
-
Автор:
bruiserdixon - 6 лет назад
-
0
-
-
Лопиталя не походили, на 2 курсе то
-
Автор:
elisechapman - 6 лет назад
-
0
-
-
Другой способ пока не приходит в голову:
Значит можно применить правило Лопиталя
-
Автор:
kate79 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
ПОМОГИТЕ ПРОШУ!!!!!!!! 7 КЛАСС АЛГЕБРА!!!!!!
Постройте треугольник МКР, если М (-4,3), К(5;1), Р(0;-4). -
25*3+36 и (12+35)*3
поставить знак больше меньше-
Предмет:
Математика -
Автор:
lincolnvvya - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Какую роль играет информатика в моей профессии?
Надо написать сочинение. (профессия ПРОГРАММИСТ)-
Предмет:
Русский язык -
Автор:
morajigq - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Какие нравственные уроки можно вывести из былины « Садко»
-
Предмет:
Литература -
Автор:
eliezer - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
