-
Найдите неопределённые интегралы . Результат проверить дифференцированием .
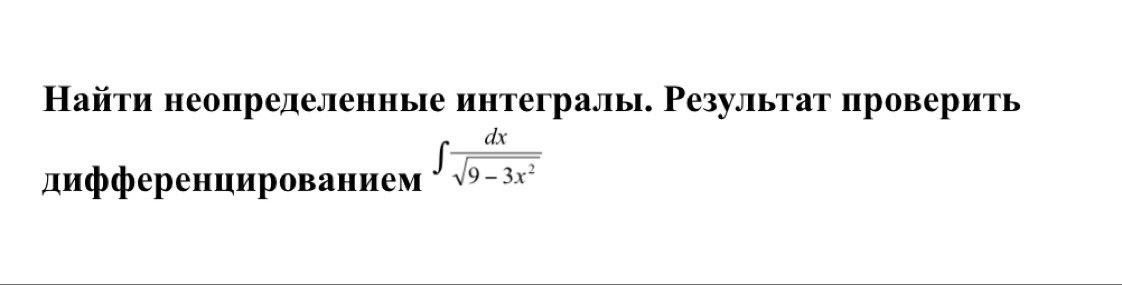
-
Предмет:
Математика -
Автор:
rachael - 6 лет назад
-
Ответы 2
Еще вопросы
-
Сколько км занимает литосфера ?
Сколько км занимает гидросфера?
На каких оболочках земли есть биосфера ?-
Предмет:
География -
Автор:
nicoblankenship - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дам 20 баллов за правильный ответ: "При каком значении Х сумма [tex]\frac{x}{3}[/tex] +[tex]\frac{2x-1}{4}[/tex] больше разности[tex]\frac{x}{2}[/tex] -[tex]\frac{1-3x}{6}[/tex] на 2"
-
Предмет:
Математика -
Автор:
jeremy5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Плизз
Помогите с заданием нужно выбрать слова из скобок-
Предмет:
Английский язык -
Автор:
tristianbrowning - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
в результаті дії сульфатної кислоти на 10 грам сплаву магнію і аргентуму виділилось 5 літрів водню. Визначити маси металів у сплаві
-
Предмет:
Химия -
Автор:
sailormcpherson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
