-
Доказать математической индукцией. Помогите, пожалуйста.
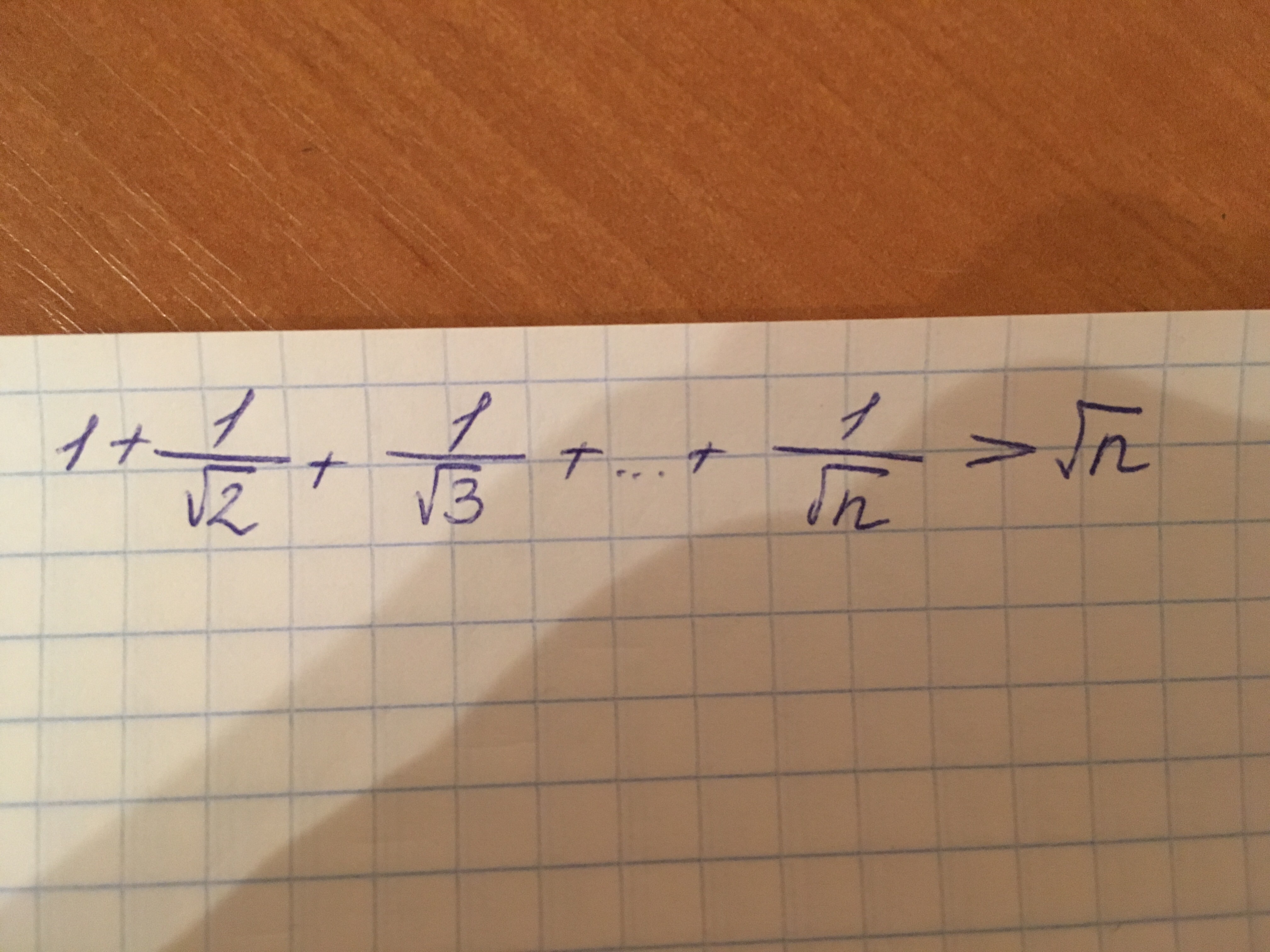
-
Предмет:
Математика -
Автор:
purdy - 6 лет назад
-
Ответы 1
-
Для n=2 неравенство верно , тогда для k=n+1 также должно быть верным
Пусть вся сумма равна S и S>sqrt(n) тогда надо доказать S+1/sqrt(n+1)>sqrt(n+1)
Откуда
S*(n+1)>sqrt(n+1)*n
Учитывая S>sqrt(n) то
S*(n+1)>(n+1)*sqrt(n)>sqrt(n+1)*n
Что верно так как
(n+1)*sqrt(n)>sqrt(n+1)*n sqrt(n+1)>sqrt(n)
n+1>n
-
Автор:
ingridserrano - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
49.•Начертите отрезки EF и ВК так,чтобы ЕF =9cм 2 мм, ВК = 7см 6мм
-
Предмет:
Математика -
Автор:
marcella - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
РЕБЯТА СРОЧНО !!! помогите
РЕБЯТА СРОЧНО
НУЖНО УКАЗАТЬ ПРЕДЛОЖЕНИЯ С ОБОСОБЛЕННЫМИ ОБСТОЯТЕЛЬСТВАМИ-
Предмет:
Русский язык -
Автор:
turtletvj3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
this is me.I m on holidays in the garden. It's sunni. I sai play in the sunny. I have a good time.I love my summer holidays. Русскими буквами по произношению что бы прочитать англиискии текст.
-
Предмет:
Английский язык -
Автор:
baby boo0d2y - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1бирл.мын ×10тени неше б
-
Предмет:
Математика -
Автор:
shania - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
