Задать вопрос Регистрация
Помочь другим

  • Привет! Помогите пожалуйста найти область определения функции(желательно с фото). Дам 15 баллов.

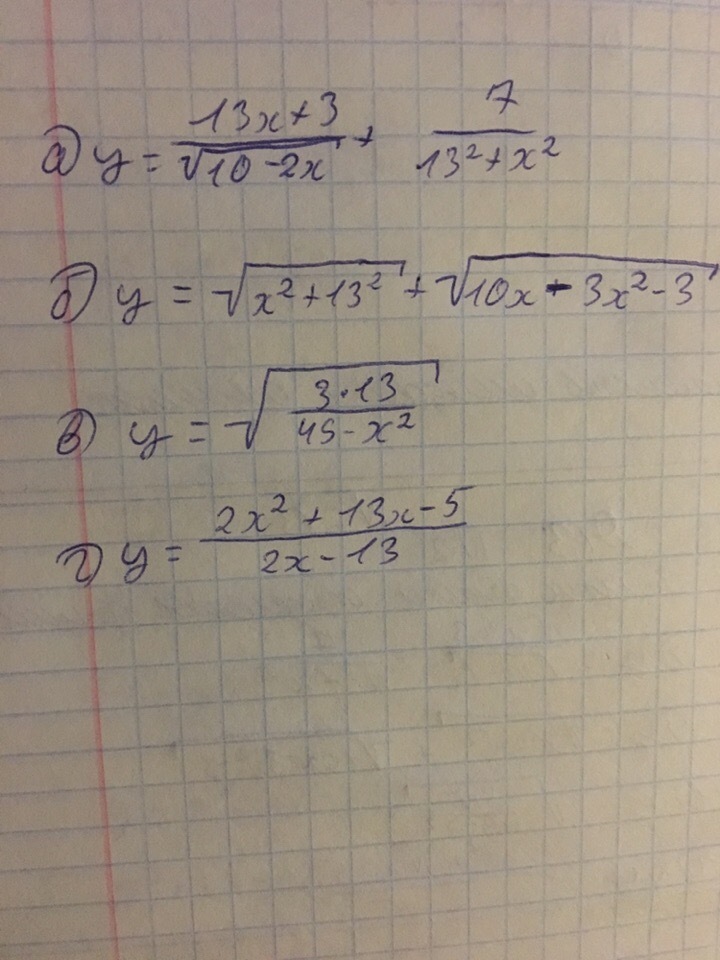
    question img

Ответы 3

  • Спасибо большое

    • Автор:

      jacob89
    • 6 лет назад
    • 0
  • ;)

    • Автор:

      xavier355
    • 6 лет назад
    • 0
  • (1)y = \frac{13x + 3}{ \sqrt{10 - 2x} } + \frac{7}{ {13}^{2} + {x}^{2} } 10 - 2x > 0 = > x < 5 {13}^{2} + {x}^{2} ≠0при любых хпоэтому Ответ:область определениях€( -∞; 5 )(2)y = \sqrt{ {13}^{2} + {x}^{2} } + \\ + \sqrt{10x - 3 {x}^{2} - 3} 13²+х²всегда >010x - 3 {x}^{2} - 3 \geqslant 0 \\ 3 {x}^{2} - 10x + 3 \leqslant 0 \\ решим3 {x}^{2} - 10x + 3 = 0x_{1,2}= \frac{10±8}{6} x_1 = 3 \\ x_2 = \frac{1}{3} наше неравенство решаем методом интервалом (см рисунок1)Ответ:область определенияx€[ ⅓; 3 ](3)y = \sqrt{ \frac{3 \times 13}{45 - {x}^{2} } } 45 - {x}^{2} > 0 \\ (3 \sqrt{5} - x)(3 \sqrt{5} + x) > 0 \\ (x - 3 \sqrt{5} )(x + 3 \sqrt{5} ) < 0опять прибегаем к методу интерваловдля решения неравенствасм рисунок 2Ответ:область определенияx€(-3√5; 3√5)(4)y = \frac{2 {x}^{2} - 13x - 5 }{2x - 13} 2x-13≠0x≠6,5Ответ:область определенияx€(-∞; 6,5) v(6,5; +∞)
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years