-
Постройте фигуру и вычислите её площадь, если фигура ограниченна линиями.
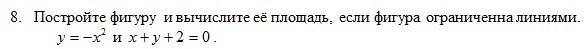

-
Предмет:
Математика -
Автор:
makhi - 6 лет назад
-
Ответы 1
-
ДАНО: y(x) = - x², f(x) = -x - 2
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
1. Графики функций на рисунке в приложении.
2. Находим пределы интегрирования решив уравнение: - x² = - x - 2, a = 2 - верхний, b = -1 - нижний предел.
3. Пишем уравнение разности функций - парабола выше прямой.
s(x) = 2 + x - x² - первообразная функция.
4. S(x) = 2*x + 1/2*x² - 1/3*x³ - интеграл - площадь
5. Вычисляем. S(2) = 4 + 2 - 2 2/3 = 3 1/3 и S(-1) = -2 + 0.5 - 1/3 = - 1 1/6
Окончательно: S = 3 1/3 + 1 1/6 = 4 1/2 = 4.5 - площадь - ОТВЕТ
ДАНО: y(x) = - x² + 2*x + 8, f(x) = -2*x 4
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
1. Графики функций на рисунке в приложении.
2. Находим пределы интегрирования решив уравнение: x² - 4 =0,
a = 2 - верхний, b = -2 - нижний предел.
3. Пишем уравнение разности функций - парабола выше прямой.
s(x) = 4 - x² - первообразная функция.
4. S(x) = 4*x - 1/3*x³ - интеграл - площадь
5. Вычисляем. S(2) = 8 - 2 2/3 = 5 1/3 и S(-2) = -8 - 2 2/3 = - 5 1/3
Окончательно: S = 5 1/3 + 5 1/3 = 10 2/3 - площадь - ОТВЕТ (≈10.667)

-
Автор:
fernando - 6 лет назад
-
0
-
-
Добавить свой ответ
-
1. Как вы думаете, почему падает активность избирателей на выборах? Какими могут быть последствия этого явления для общества, государства, личности?
2. Что влияет на выбор человека? Назовите 3 наиболее важных, по вашему мнению, фактора
3. Существует мнение - когда ты не голосуешь, на самом деле ты все-таки голосуешь. Согласны ли вы с этим мнением? Почему?
4 Знаменитый итальянский мыслитель эпохи возрождения Николло Макиавелли утверждал, что для достижения политических целей хороши все средства: ложь, предательство, подлость, коварство, пытки, убийства. Согласны ли вы с этой точкой зрения? Почему?
5 Житейская мудрость гласит: "Если вы не хотите заниматься политикой, она займется вами" Согласны ли вы с этим? Почему?-
Предмет:
Обществознание -
Автор:
marqueshinton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какие слова Андрия в разговоре с полячкой поражают вас больше всего? Почему? Помогите быстрее
-
Предмет:
Литература -
Автор:
princessxmhh - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
бісектриса одного з кутів гострокутного трикутника дорівнює з висотою проведеною з тієї самої вершини кут який дорівнює 10градусів а один з двох інших кутів трикутника дорівнює 70грудусів. знайдіть невідомі кути трикутника
-
Предмет:
Геометрия -
Автор:
lizethbxhy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
y=5-2x,Пусть x= -3.Тогда y=?
-
Предмет:
Математика -
Автор:
vidalbarton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
