-
Помогите, срочно! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
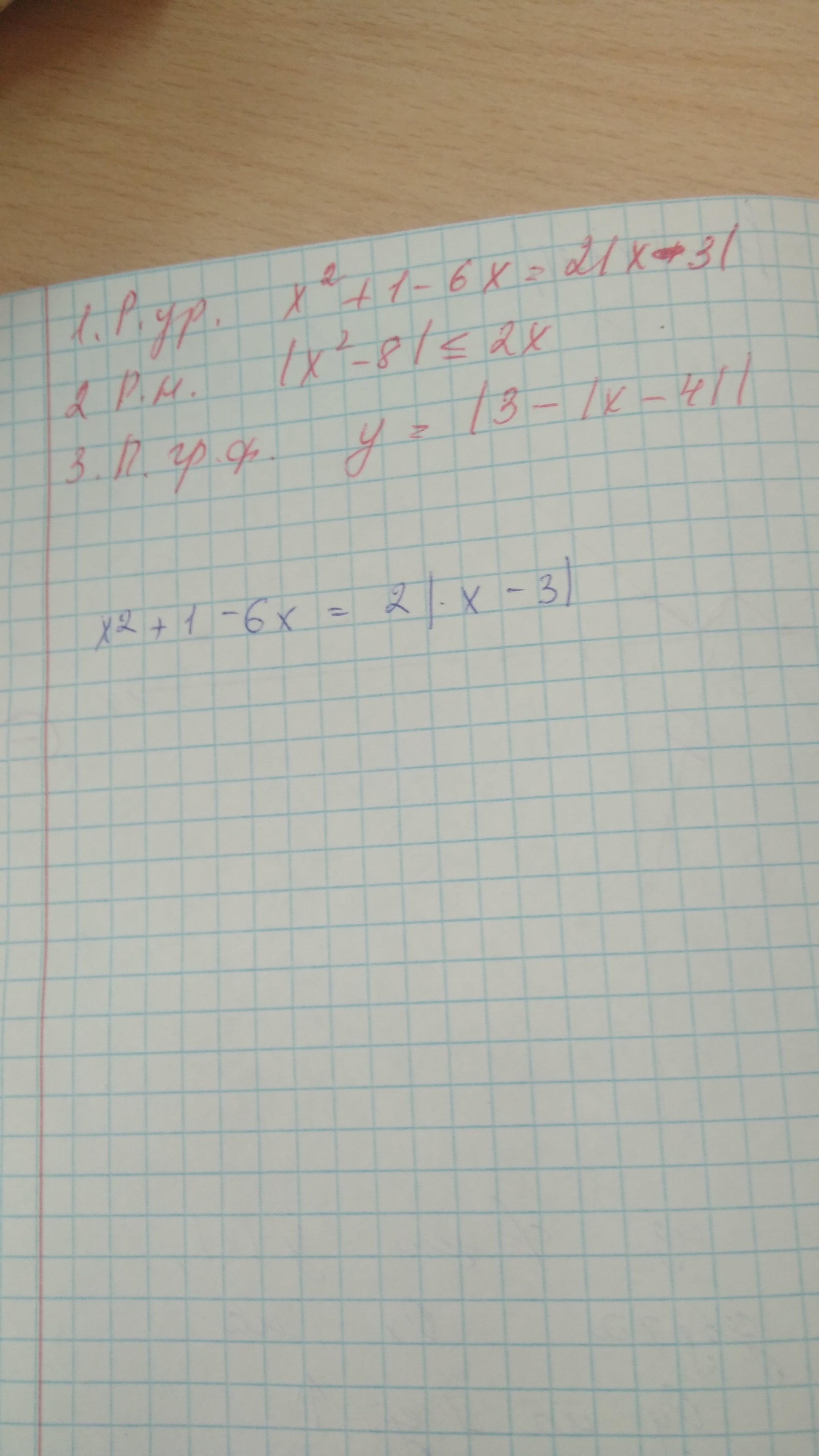
-
Предмет:
Математика -
Автор:
efrainhardin - 6 лет назад
-
Ответы 1
-
Сначала строим график y=|x| .Затем сдвигаем его относительно оси ОХ вправо на 4 единицы, получаем график y=|x-4| . Потом отображаем этот график относительно оси ОХ, получаем график y=-|x-4| . Поднимаем этот график на 3 единицы вверх вдоль оси ОУ, получаем график y=3-|x-4|. А затем ту часть графика, которая находилась ниже оси ОХ, отображаем относительно ОХ в верхнюю полуплоскость, получим график y=|3-|x-4|| . На рисунке красный график.

-
Автор:
big footrussell - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Аналогичные органы
А.передняя конечность летучий мыши и крыло птицы
Б.передняя конечность лягушки и крыло птицы
В.крыло бабочки и крыло птицы
Г.усики гороха и колючки кактуса -
звонит поставьте ударение
-
Предмет:
Русский язык -
Автор:
peppyunjm - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
complete each sentence with a verb in the correct form - ing or to
-
Предмет:
Английский язык -
Автор:
yakaddqn - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Как влияет температура на скорость движения молекул вещества?
How much to ban the user?
1 hour
1 day
100 years
