Задать вопрос Регистрация
Помочь другим

  • Найти область сходимости степенного ряда (задание на фото):

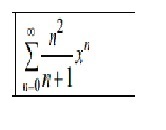
    question img

Ответы 1

  • Радиус сходимости \sf \displaystyle R=\lim_{n \to \infty} \dfrac{a_n}{a_{n+1}}=\lim_{n \to \infty}\dfrac{n^2}{n+1}\cdot\frac{n+2}{(n+1)^2}=1

    ряд сходится при всех х ∈ (-1;1).

    Исследуем сходимость ряда на концах интервала (-1;1).

    Если x=-1, то

    \displaystyle \sum^{\infty}_{n=0}\frac{(-1)^n\cdot n^2}{n+1} - расходится по признаку Лейбница.

    Если x=1, то \displaystyle\sum^{\infty}_{n=0}\frac{n^2}{n+1} -расходится, так как не выполняется необходимое условие сходимости ряда.

    Ответ: ряд сходится абсолютно при x ∈ (-1;1).

    • Автор:

      cruella
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years