-
Исследовать функцию и построить график
y=x-4/x^2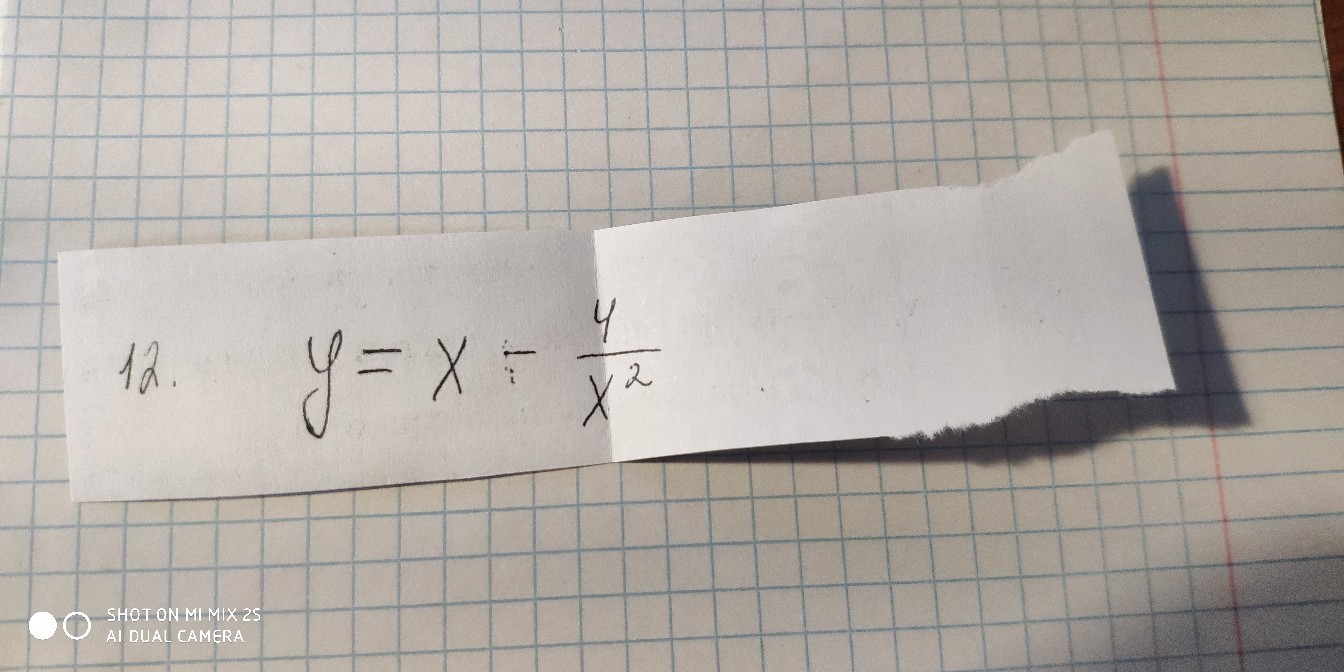
-
Предмет:
Математика -
Автор:
sandy - 6 лет назад
-
Ответы 4
-
функция, что вы представили в решении, не совсем совпадает с данной в условии
-
Автор:
mosesxolu - 6 лет назад
-
0
-
-
Да. Надо минус четыре.
-
Автор:
tinky - 6 лет назад
-
0
-
-
ИСПРАВЛЕНО
-
Автор:
aniya - 6 лет назад
-
0
-
-
ДАНО: Y = (x³-4)/x²
ИССЛЕДОВАТЬ.
1.Область определения D(x) - x²≠ 0 - разрыв при Х =0.
Вертикальная асимптота: X = 0.
D(x) - Х∈(-∞;0)∪(0;+∞).
2. Пересечение с осью Х.
x³ -4 = 0 при х = ∛4 ≈ 1.6.
3. Пересечение с осью У – нет – функция не существует.
Интервалы знакопостоянства.
Отрицательна: Х∈(-∞;0)∪(0;∛4).
Положительна: Х∈(∛4;+∞). .
4. Поведение на бесконечности. limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальных асимптот - нет.
5. Исследование на чётность.
Y(-x) = (-x³+4)/x² ≠ - Y(x). Y(-x) = -(-x³+4)/x² ≠ - Y(-x).
Функция ни чётная ни нечётная.
6. Производная функции.
Y’(x) = 1 + 8/x³=0 x= ∛8 = -2
7. Локальные экстремумы.
Максимум – y(-2) = - 3. Минимума – нет.
8. Интервалы монотонности.
Возрастает: X∈(-∞;-2)∪(0;+∞), убывает - Х∈(-2;0)
9. Вторая производная- Y"(x) = 24/x = 0.
10. Точек перегиба - нет (Только в точке разрыва - Х =0)
Выпуклая - "горка" - Х∈(-∞;0). Вогнутая – «ложка» Х∈(0;+∞).
11. Область значений Е(у) У∈(-∞;+∞)
12. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
k=lim(∞)Y(x)/x³ = 1 – разделили на х3 -
F(x) = (x - 4/x²)/(x²/x²) = x. (Разделили на х2)
Уравнение наклонной асимптоты F(x) = x.
13. График в приложении

-
Автор:
angie - 6 лет назад
-
0
-
-
Добавить свой ответ
- на одной полке на 15 книг больше чем на другой. всего на двух полках 53 книги. сколько книг на каждой полке. решите пж. это за 7 класс.
-
Раздел науки о языке, изучающий слово и его лекическое значение как называется?пожалуйста скажитее
-
Предмет:
Русский язык -
Автор:
knucklebutt - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
умоляю помогите срочно пожалуйста,очень срочно номер 7 и 8
-
Предмет:
Английский язык -
Автор:
peppermint - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Генетика:
Кареглазость-А
Голубоглазость-а
Правша-В
Левша-в
Он-кареглазый правша,( у которого мама-голубоглазая правша, а отец- кареглазый правша), она-голубоглазая левша
Найти-F1?-
Предмет:
Биология -
Автор:
addysondne7 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
