Задать вопрос Регистрация
Помочь другим

  • Найти экстремумы функции

    1/4(x-3)^2(x+3)

    Подробно молю, пожалуйста.
    Вся сложность в взятии производной..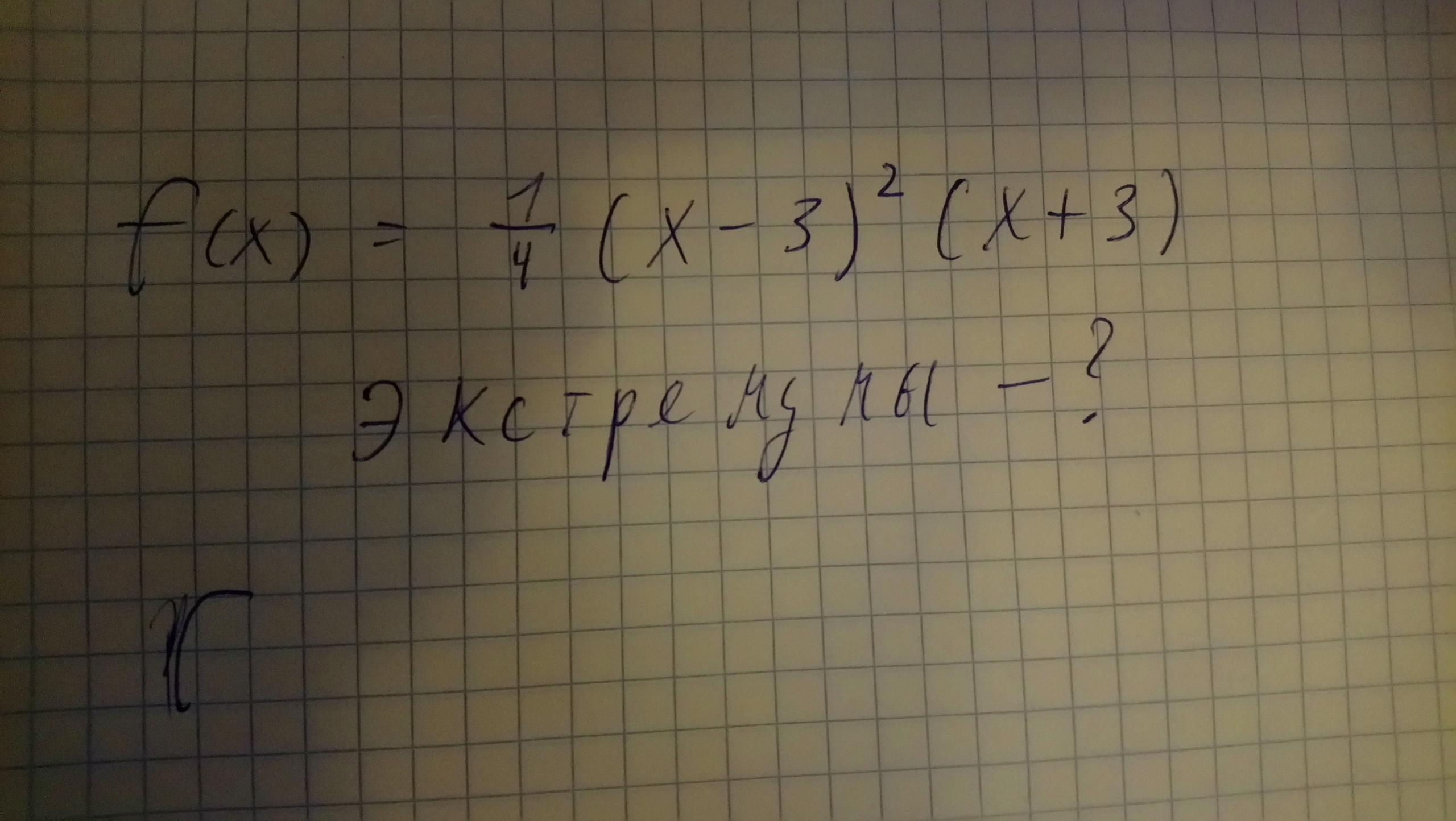

    question img

Ответы 1

  • Точка называется экстремумом функции если производная функции в этой точке равна нулю.

    f(x)= \frac{1}{4} * (x-3)^{2} *(x+3)=\frac{1}{4} *(x-3)*(x-3)*(x+3)=\frac{1}{4}* (x^{3}-9x-3 x^{2} +27)\\f'(x)=\frac{1}{4}*(3x^{2}-9-6x)

    f'(x)=0\\x^{2} -2x-3=0\\x_{1} = 3\\ x_{2} = -1.

    Проверяем, какая из точек является минимумом функции f(x), а какая максимумом.

    Если при переходе через точку x1 производная функции меняет знак с плюса на минус, то х1 - точка масимума функции, если с минуса на плюс, то х1 - точка минимума функции.

    f'(-2)= \frac{1}{4} *(3*4-9+12)=15/4 -знак +

    f'(0) = -9/4 - знак минус

    f'(4)=\frac{1}{4} *(3*16-9-24)=\frac{15}{4} - знак плюс

    Таким образом

    f(-1)= \frac{1}{4} * 16*2=8 - максимум функции

    f(3) = 0 - минимум функции

    • Автор:

      monserrat
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years