Задать вопрос Регистрация
Помочь другим

  • Освободитесь от иррациональности в знаменателе дроби помогите срочно

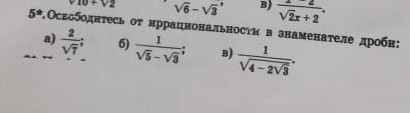
    question img

Ответы 4

  • Спасибо
  • Удачи в учёбе :)

    • Автор:

      lillianna
    • 5 лет назад
    • 0
  • Спасибо :)
  • Избавиться от иррациональности.# 1. Простое домножение до квадрата

    \dfrac{2}{\sqrt7} = \dfrac{2\sqrt7}{(\sqrt7)^2} = \dfrac{2\sqrt7}{7}.

    # 2. Домножение на сопряженное.

    \dfrac{1}{\sqrt5-\sqrt3} = \dfrac{\sqrt5+\sqrt3}{(\sqrt5-\sqrt3)(\sqrt5+\sqrt3)} = \dfrac{\sqrt5+\sqrt3}{(\sqrt5)^2-(\sqrt3)^2} = \dfrac{\sqrt5+\sqrt3}{5 - 3} = \dfrac{\sqrt5+\sqrt3}{2}.

    # 3. Увидеть квадрат разности и тоже, что в 2.

    \dfrac{1}{\sqrt{4-2\sqrt{3}}} = \dfrac{1}{\sqrt{1^2 + (\sqrt3)^2 - 2\sqrt3}} = \dfrac{1}{\sqrt{(1 - \sqrt3)^2}} = \dfrac{1}{|1 - \sqrt{3}|} =\\\\= \dfrac{1}{\sqrt3 - 1} = \dfrac{\sqrt3 + 1}{(\sqrt3 - 1)(\sqrt3 + 1)} = \dfrac{\sqrt3 + 1}{3 - 1} = \dfrac{\sqrt3 + 1}{2}.

    Раскрывая квадратный корень от квадрата, нельзя забывать, что подкоренное выражение всегда неотрицательно поэтому нужно писать модуль.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years