y'-2y,-2y/x=1+1/x Всё, что дано Можете делать с этим, что хотите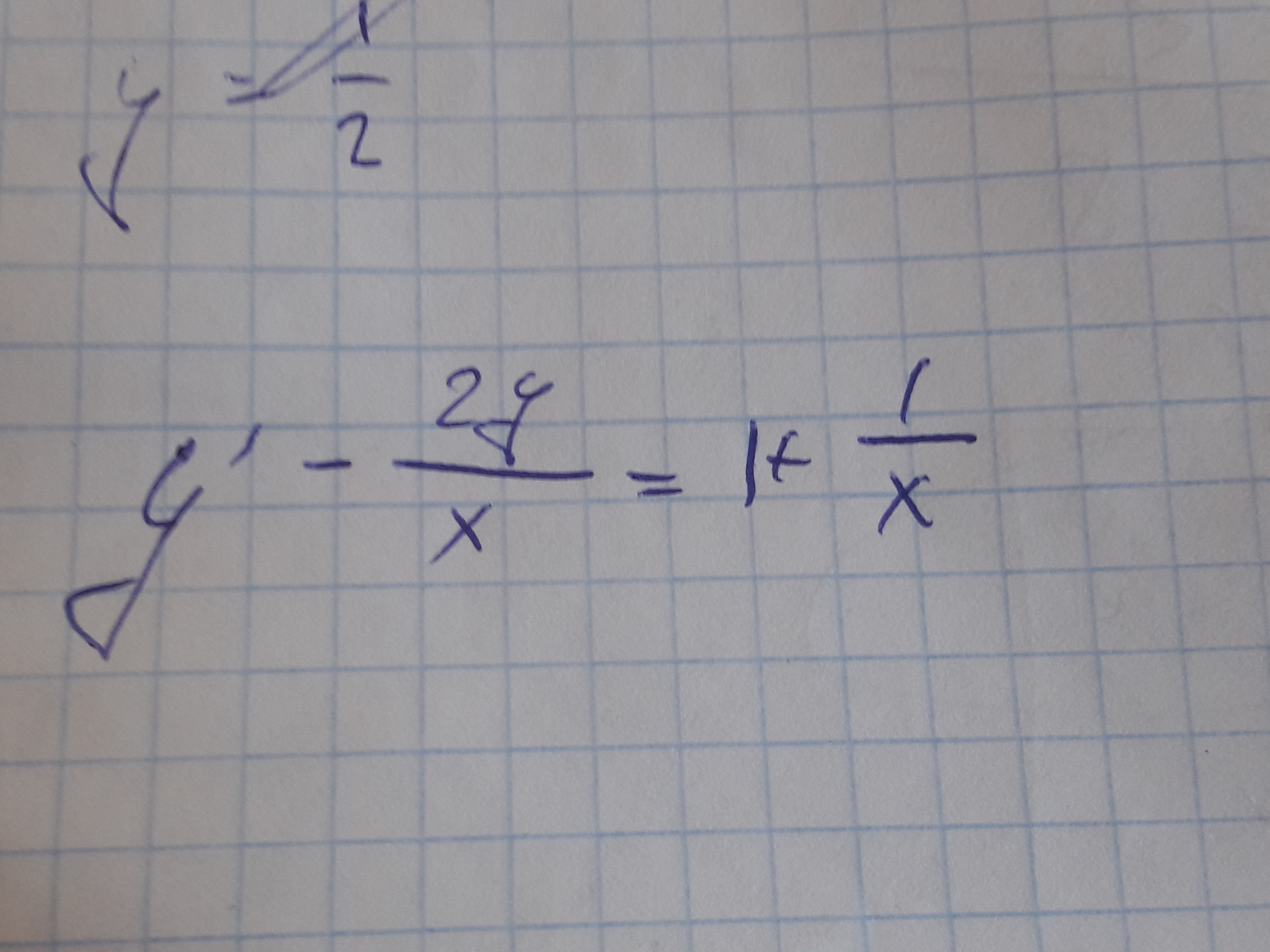 - №30481627

y'-2y,-2y/x=1+1/x
Всё, что дано
Можете делать с этим, что хотите
- Предмет:
  Математика
- Автор:
  tank82
- 6 лет назад

Ответы 1

У Вас задано линейное неоднородное дифференциальное уравнение. Его можно решать либо методом вариации постоянной, либо подставновкой вида y=u*v. Воспользуемся вторым методом:
$y'-\frac{2y}{x}=1+\frac{1}{x}$
$(u*v)'-2*u*v/x=1+1\x\\\\u'v+v'u-2uv/x=1+1/x$
$u'v+u(v'-2v/x)=1+1/x$
Найдём частное решение однородного уравнения, т.е.
$v'-2v/x=0\\\\dv/v=2dx/x\\\\ln|v|+C_1=2ln|x|+C_2$
Возьмём частное решение при $C_2-C_1=0$ , т.е. $v=x^2$ .
Вернёмся к исходному уравнению, и подставим найдённое v:
$u'x^2+u*0=1+1/x\\\\du/dx=(1/x^3+1/x^2)\\\\u=-\frac{1}{2x^2}-\frac{1}{x}+C$
Тогда, возвращаясь к введённой нами замене, получим:
$y=u*v=(-1/2x^2 -1/x + C)x^2=Cx^2-x-0.5$
- Автор:
  kato
- 6 лет назад
- 0
Добавить свой ответ

Еще вопросы

How much to ban the user?

1 hour 1 day 100 years