-
Не могу решить простой предел(без использования правила Лопиталя).
Изначальный предел имеет вид:
Lim(x->бесконечности) (Sqrt(x^2 +2)-sqrt(x^2 +7))
Преобразовал до вида(прикладываю картинку).
После решал через вынос x из обоих корней и ответ получал 0, но решение не приняли, хоть и ответ правильный. Не доходит до меня, что надо сделать с корнями :/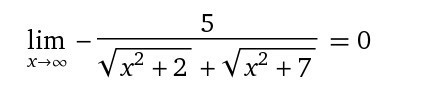
-
Предмет:
Математика -
Автор:
mohammed - 6 лет назад
-
Ответы 12
-
Не обязательно неопределенность {inf/inf}. Для стремящихся к бесконечности можно разделить
-
Автор:
gusmack - 6 лет назад
-
0
-
-
Могли бы вынести в знаменателе за скобки х, и выделить 5/х в числитель....
-
Автор:
captainuqvr - 6 лет назад
-
0
-
-
Мы отдельно делим 5/x и отдельно в корнях 2/х и 7/х
-
Автор:
marques7afb - 6 лет назад
-
0
-
-
В числителе же получится 5/(x^2), это не изменит решения?
-
Автор:
payten30 - 6 лет назад
-
0
-
-
Как будет правильнее вынести в знаменателе за скобки x?
-
Автор:
audreymitchell - 6 лет назад
-
0
-
-
Почему в знаменателе x^2
-
Автор:
brennan - 6 лет назад
-
0
-
-
Мы же сокращаем всю дробь на x^2, в знаменатели тем самым сокращаем x^2 оба и получаем дроби как у вас в ответе, а у 5 нет же икса, чтобы сократить его и получить знаменатель просто x, без степени
-
Автор:
arniescott - 6 лет назад
-
0
-
-
Вынести можно ~так
-
Автор:
elianna - 6 лет назад
-
0
-
-
Если вы x под корень внесёте, то он возведётся в квадрат
-
Автор:
jorgewashington - 6 лет назад
-
0
-
-
Точно, спасибо)
-
Автор:
tiannasampson - 6 лет назад
-
0
-
-
Разделите дробь на х (на старший степень х).
-
Автор:
norberto - 6 лет назад
-
0
-
-
-
Автор:
cold brewifek - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
№ 459:
Пусть a-основание,h-высота,а S-площадь параллелограмма. Найдите S,если a=15 см,h=12 см.-
Предмет:
Геометрия -
Автор:
finneganbaxter - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить пожалуйста. Под номером 446 номер 2 и под номером 447 номер 2
-
Предмет:
Математика -
Автор:
juliehorton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Водородная связь может образовываться между молекулами:
а)метана; б)аммиака; в)азота; г)фтороводорода.-
Предмет:
Химия -
Автор:
everettsimon - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Зазначте яка речовина утворюється на першій стадії хлорування етану:
А) хлоретан
Б) 1,1-дихлоретан
В)1,2-дихлоретан
Напишіть рівняння реакції
How much to ban the user?
1 hour
1 day
100 years
