-
НА ПОМОЩЬ !!!
Из вершины C прямоугольного треугольника abc(c=90) проведен перпендикуляр CD к его плоскостям. Найти длинy наклонных AD и BD а так же длину перпендикуляра CD при следующих длинах:
Угол CAB 30°
Угол ADC 45°
AC 20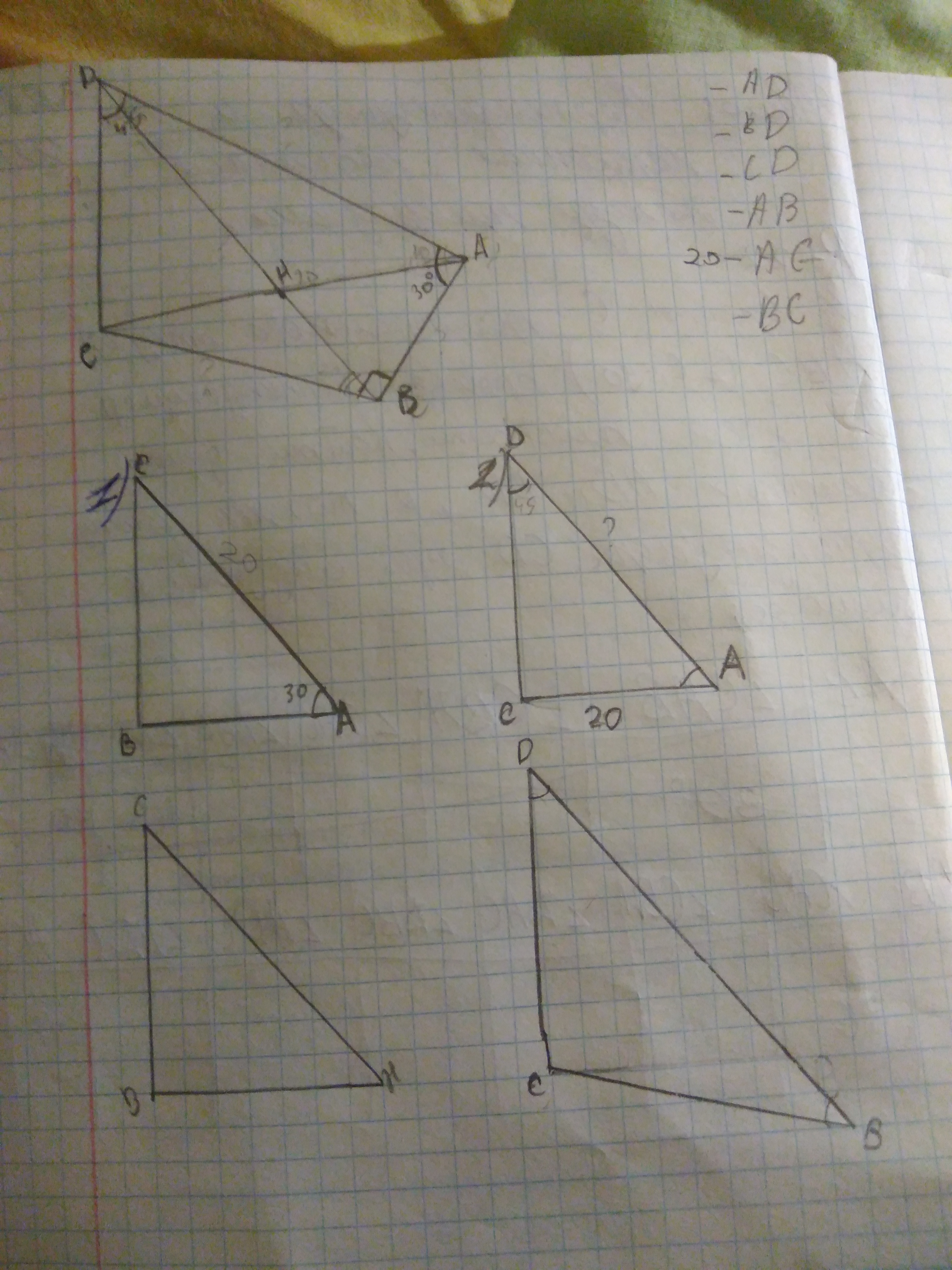
-
Предмет:
Математика -
Автор:
justus - 6 лет назад
-
Ответы 2
-
Ответ:
Пошаговое объяснение:

-
Автор:
hendrix - 6 лет назад
-
0
-
-
task/30605008
Дано ΔABC : ∠ACB =90° ; CD⊥ (ABC) ; ∠CAB =30° ; ∠ADC =45° ; AC =20 . -----------
AD -? , BD - ? CD - ?
решение : Треугольники ACD и ВCD прямоугольные , т.к. DC ⊥ (ABC) ⇒ DC ⊥ CA и DC ⊥ СВ .
Из ΔACD: ∠ADC =45° ⇒ ∠DAC =90° - ∠ADC =90° - 45°= 45° , поэтому прямоугольный треугольник ACD еще и равнобедренный CD = CA =20 . AD =√(CA²+CD²) = √(CA²+CA²) =√(2CA²) =CA√2 = 20√2 .
В ΔABC : CB = AB/2 (как катет против угла 30°) ⇒ AB =2СВ ; по теореме Пифагора: AC=√(AB² - CB²) = √( (2CB)² - CB²) = √( 4CB² - CB²) =√(3CB²) = CB√3 ⇒ CB = AC/√3 =20 /√3 || AB =2CB =40/√3 ||
Из ΔBCD: BD =√(BC²+DC²) =√( (20/√3)²+20²) =√( 20²(1/3+1 )=√( 20²*4/3 ) = 20*2 /√3 = 40 /√3 =(40√3) /3 .
Ответ: AD = 20√2 ; BD =(40√3) /3 ; CD =20 .
P.S. ! ΔCDB = ΔCAB ( CA _общий катет и CD=AC ⇒ BD=AB )

-
Автор:
kian - 6 лет назад
-
0
-
-
Добавить свой ответ
-
разделите число 90 на две части так чтобы 40% в одной части были на 15 больше 30% другой части в Ответ запишите больший из этих частей. С подробным решением пожалуйста. Тот вариант решения что был на данном портале не расматриваю. Число 90 делят на две части, а не на три как до этого в решении.
-
Предмет:
Математика -
Автор:
simone5fpq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите с монологом пожалуйстааа
1.What kinds of food people eat in your country?
2.Whether most people have a healthy diet,why/why not?
3.Whether you prefer eating at home or eating out,why?
4.What food you eat on special occasions,why?
-
Предмет:
Английский язык -
Автор:
mcguire - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Глаголы стихотворения Улыбка Улбике
Б.Каирбекова
Помогите
-
Предмет:
Русский язык -
Автор:
charity - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОЖАЛУЙСТА ПОМОГИТЕ СРОЧНО!!!
Напишите (визитную) карточку про Яна Гуса, а точнее про него и гуситские войны!
