Задать вопрос Регистрация
Помочь другим

  • Комбинаторика.

    Решить уравнение: под цифрой 9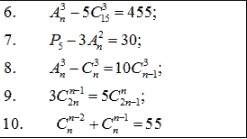

    question img

Ответы 1

  • Ответ: n=5

    Пошаговое объяснение:

    \frac{3(2n)!}{(n-1)!(2n-n+1)!}=\frac{5(2n-1)!}{n!(2n-1-n)!}\\\frac{3(2n)!}{(n-1)!(n+1)!}=\frac{5(2n-1)!}{n!(n-1)!}\\

    Перенесём дроби в одну часть (левую) и вынесем общий множитель.

    \frac{(2n-1)!}{n!(n-1)!}\left(\frac{3(2n)}{n+1}-5ight)=0

    Т.к. факториал принимает значения от 1 до плюс бесконечности, то равенство может обратиться в ноль только благодаря разности в скобке.

    \frac{6n}{n+1}-5=0\\\\\frac{6n-5n-5}{n+1}=0\\\-5=0 => n=5

    Сделаем проверку:

    \frac{3(10)!}{4!6!}=\frac{3*7*8*9*10}{2*3*4}=7*9*10=630\\\\\frac{5*9!}{4!5!}=\frac{5*6*7*8*9}{2*3*4}=3*5*6*7=630

    • Автор:

      jenkins
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years