-
Исследовать функцию y=f(x) на непрерывность. Найти
точки разрыва функции и определить их тип. Построить схематический
график функции.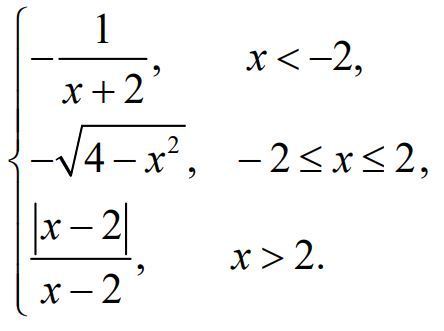
-
Предмет:
Математика -
Автор:
biscuithenderson - 6 лет назад
-
Ответы 1
-
Пошаговое объяснение:
1. ДАНО: Y = - 1/(x+2), X∈(-∞;-2) или D(y) = {-∞;-2}
x+2 ≠0, X≠ -2 - разрыв не входит в область определения. Вертикальная асимптота - Х = -2.
Получаем одну ветвь графика - Y = - 1/(x+2), Поведение на бесконечности: Y(-∞) = 0, limY(x->-2) = +∞. Вычисляем, например при Х = - 2,5 и получаем Y(-2.5) = 2
3. Разрыв при Х=2 - могла бы быть вертикальная асимптота, но область определения - правая часть графика - красная.
График на рисунке в приложении.
2. ДАНО: Y = - √(4 - x²), D(y) ={-2;2}.
Под корнем - неотрицательное число, как раз в области определения. Значения х = +/-2 - исключаем - "дырки". Сам корень - положительный, на графике становится отрицательным.
Под корнем - х ² - на графике - два фрагмента графика корня.
3.

-
Автор:
dante68 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Что такое КПД по физике
-
Предмет:
Физика -
Автор:
cordelld5ic - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Как сделать слово "огонь" С суффиксом 'ек или ик' в единственном числе и множественном.
-
Предмет:
Русский язык -
Автор:
cole58 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
25 баллов. Ничего не требуется просто объясните как из 0.35 получилось 0.65, а из 0.45 получилось 0.55. Найти нужно было плановые объемы валовой продукции отраслей
-
Предмет:
Математика -
Автор:
porfiriorobbins - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Что такое дактилическая рифма?Плииззз приведите пример☺️☺️☺️
-
Предмет:
Литература -
Автор:
carina65 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
