-
Помогите, пожалуйста,решить! Задание егэ №15 (логарифмы)
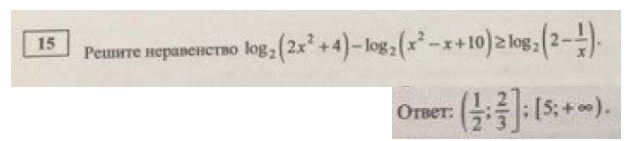
-
Предмет:
Математика -
Автор:
buffy - 6 лет назад
-
Ответы 1
-
Находим ОДЗ: 2х² + 4 всегда больше нуля.
х² - х + 10. Д = 1 - 4*10 = -39. Так как коэффициент при х² положителен, то вся функция лежит в положительной полуплоскости.
2 - (1/х) > 0, 2 > (1/х), x > 1/2.
По свойству логарифмов при одинаковом основании:
Приведём к общему знаменателю и перенесём правую часть налево.
Получили неравенство 3х² - 17х + 10 ≥ 0.
Находим нули функции из условия 3х² - 17х + 10 = 0.
Ищем дискриминант:
D=(-17)^2-4*3*10=289-4*3*10=289-12*10=289-120=169;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√169-(-17))/(2*3)=(13-(-17))/(2*3)=(13+17)/(2*3)=30/(2*3)=30/6=5;
x_2=(-√169-(-17))/(2*3)=(-13-(-17))/(2*3)=(-13+17)/(2*3)=4/(2*3)=4/6=2/3.
По свойству параболы значения больше нуля лежат левее левой и правее правой нулевых точек.
С учётом ОДЗ имеем ответ: (1/2) < x ≤ (2/3), 5 ≤ x < +∞.
-
Автор:
buckyboyd - 6 лет назад
-
0
-
-
Добавить свой ответ
-
передзим'я значення слова
-
Предмет:
Українська мова -
Автор:
jordenprince - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Составьте распростронённое предлодение со словаочитанием лазурный берег
-
Предмет:
Русский язык -
Автор:
jonathankkaj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В треугольнике FGH угол 1 равен углу 2 и равен углу 3(рис.10.16).верно ли утверждение о том,что это треугольник: а) равнобедренный; б) равносторонний; в) правильный?
-
Предмет:
Геометрия -
Автор:
dirty harry6a2j - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста решить это (x+5)²+(y-3)=25 нужно найти радиус окружности
-
Предмет:
Математика -
Автор:
timoteo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
