Задать вопрос Регистрация
Помочь другим

  • Найти указанные пределы, используя правило Лопиталя.

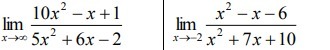
    question img

Ответы 1

  • Ответ:

    \lim_{x \to \infty} \frac{10x^2-x+1}{5x^2+6x-2}=2

    \lim_{x \to \-2} \frac{x^2-x-6}{x^2+7x+10}=-\frac{5}{3}=-1\frac{2}{3}

    Пошаговое объяснение:

    Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль или бесконечность в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

    если

    \lim_{x \to a} f(x)=\lim_{x \to a} g(x)= \infty

    или

    \lim_{x \to a} f(x)=\lim_{x \to a} g(x)= 0

    то

    \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}

    \lim_{x \to \infty} \frac{10x^2-x+1}{5x^2+6x-2}=\left [ \frac{\infty}{\infty}ight]= \lim_{x \to \infty}\frac{(10x^2-x+1)'}{(5x^2+6x-2)'}=\lim_{x \to \infty}\frac{20x-1}{10x+6}=\left [\frac{\infty}{\infty}ight] =

    =\lim_{x \to \infty}\frac{(20x-1)'}{(10x+6)'}=\lim_{x \to \infty}\frac{20}{10}=2

    \lim_{x \to \-2} \frac{x^2-x-6}{x^2+7x+10} = \left [ \frac{0}{0}ight]= \lim_{x \to \-2} \frac{(x^2-x-6)'}{(x^2+7x+10)'} =

    =\lim_{x \to \-2} \frac{2x-1}{2x+7}=\frac{2\cdot(-2)-1}{2\cdot(-2)+7}=\frac{-5}{3}=-1\frac{2}{3}

    • Автор:

      isabell
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years