-
Найти интервалы монотонности и экстремумы функции.
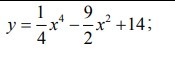
-
Предмет:
Математика -
Автор:
alexzander - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
для анализа поведения функции найдем первую производную
Найдем x, при которых y'=0/ "то точки -3, 0, 3. В них функция принимает экстремальные значения
x=-3 y=-6,25
x=0 y=14
x=3 y=-6,25
Рассмотрим поведение функции на полученных участках
x<-3 y'<0 ⇒ y монотонно убывает
-3<x<0 y'>0 ⇒ y монотонно возрастает, в точке -3 y' меняет знак с - на +, точка -3 является точкой локального минимума
0<x<3 y'>0 ⇒ y монотонно убывает, в точке 0 y' меняет знак с + на -, точка 0 является точкой локального максимума
x>3 y'>0 ⇒ y монотонно возрастает, в точке 3 y' меняет знак с - на +, точка 3 является точкой локального минимума
-
Автор:
shiner0mms - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- висновок про те яка існує відповідність мій формами рельєфу та тектонічними структурами материків
-
найвищий діючий вулкан планети
-
Предмет:
География -
Автор:
andregarza - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Какие особенности строения конечностей позволяют блохе совершать прыжки на большие расстояния?
-
Предмет:
Биология -
Автор:
willowadkins - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕЕ!
Нужно составить схему "парламента"(история 6 класс)
Помогите пожалуйстаа
Зарание спасибо!
How much to ban the user?
1 hour
1 day
100 years
