Задать вопрос Регистрация
Помочь другим

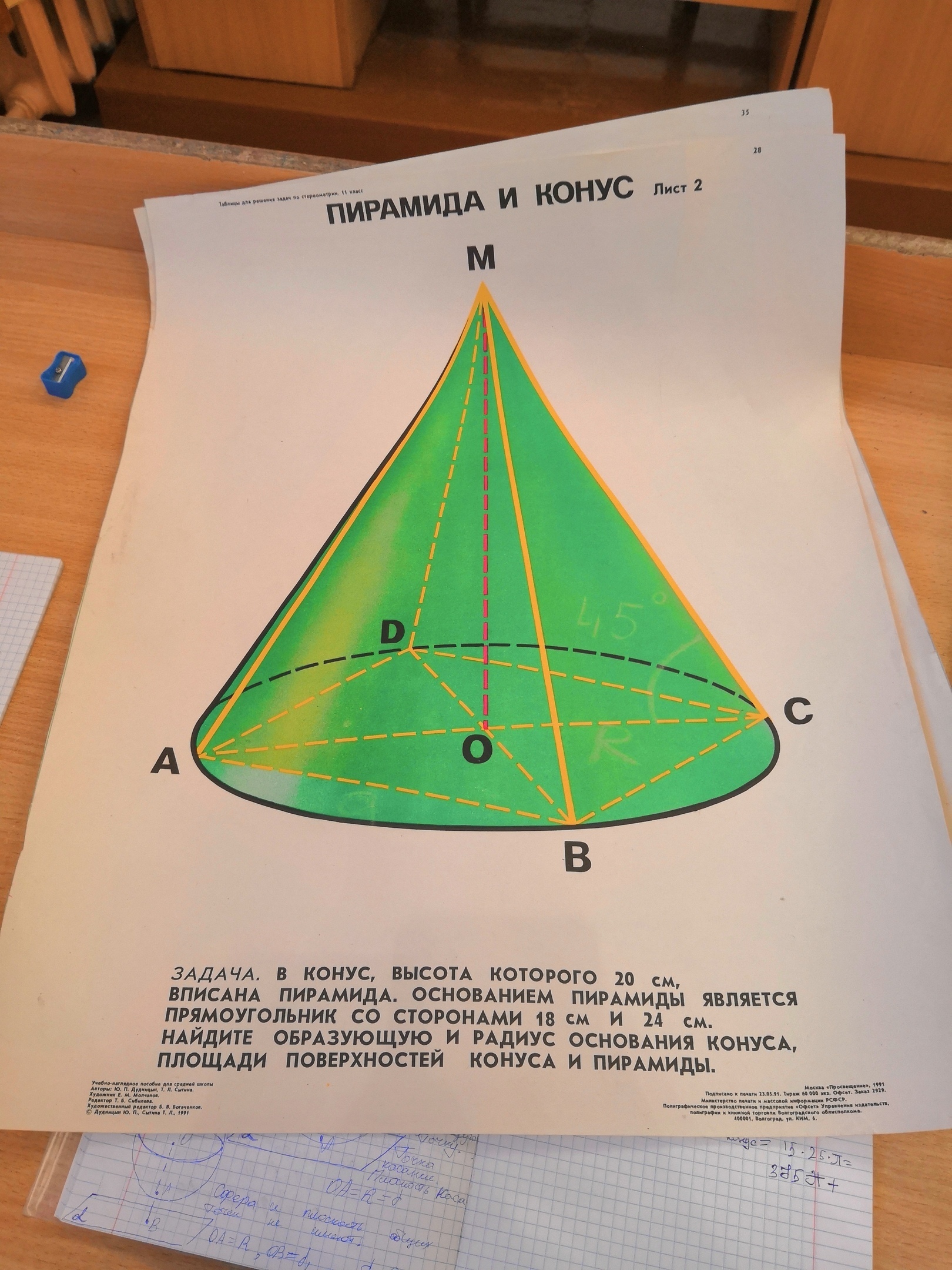
  • Решить задачу (на фото) радиус круга r = 15, Образующая MB = 25

    question img

Ответы 2

  • Так запариться - респект

    • Автор:

      hickman
    • 6 лет назад
    • 0

  • Ответ:

    Пошаговое объяснение:

    Из прямоугольного ΔADB найдем диагональ BD прямоугольника:

    BD^2=AD^2+AB^2=18^2+24^2=324+576=900\\BD=30

    Радиус основания конуса OB равен половине диагонали BD

    r = BD / 2 = 30 / 2 = 15

    Образующую конуса MB найдем из прямоугольного ΔMOB:

    MB^2=MO^2+OB^2=20^2+15^2=400+225=625\\MB=25

    l = 25

    Полную площадь поверхности конуса найдем по формуле:

    S=\pi*r(r+l)=\pi*15*(15+25)=600\pi

    Полную площадь поверхности пирамиды найдем как сумму площадей пяти ее составляющих:

    S=S_{AMB}+S_{BMC}+S_{CMD}+S_{AMD}+S_{ABCD}

    ΔAMB = ΔMCD (по трем сторонам)

    ΔBMC = ΔAMD (по трем сторонам)

    и можем переписать формулу в виде:

    S=2*S_{AMB}+2*S_{BMC}+S_{ABCD}

    В треугольнике AMB опустим высоту MH на основание AB и из прямоугольного треугольника AHM найдем ее длину:

    MH^2=AM^2-AH^2=25^2-12^2=625-144=481\\MH=\sqrt{481}

    В треугольнике BMC опустим высоту MF на основание BC и из прямоугольного треугольника BFM найдем ее длину:

    MF^2=BM^2-BF^2=25^2-9^2=625-81=544\\MF=\sqrt{544}

    Зная высоты площади треугольников AMB и BMC найдем по формуле полупроизведения основания на высоту:

    S=2*S_{AMB}+2*S_{BMC}+S_{ABCD}=AB*MH+BC*MF+AB*BC=24*\sqrt{481}+18*\sqrt{544}+24*18=24*\sqrt{481}+72*\sqrt{34}+432

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years