Задать вопрос Регистрация
Помочь другим

  • Допоможіть зробити завдання по математиці за 8 клас!! Відам усі балли!

    question img
    question img
    question img

Ответы 1

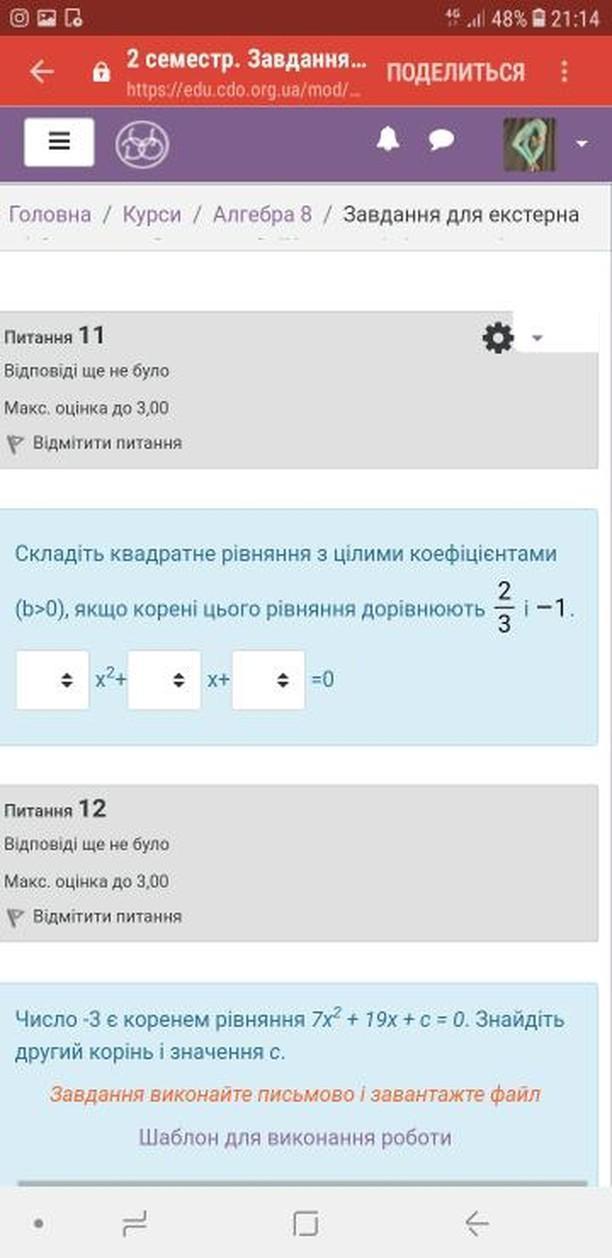
  • Питання 11.

    Якщо корені квадратного рівняння відомі x_1=\frac{2}{3},x_2=-1, то саме рівняння можна записати у вигляді:

    \left(x-\frac{2}{3}ight)(x+1)=0

    і, розкривши дужки та помноживши все рівняння на 3, отримуємо

    3x^2+x-2=0

    Також можна скористатись теоремою Вієта:

    x^2-\left(\frac{2}{3}+(-1)ight)x+\frac{2}{3}\cdot(-1)=0

    3x^2+x-2=0.

    Питання 12.

    З теореми Вієтта другий корінь рівняння буде дорівнювати:

    x_2=-\frac{19}{7}-x_1=-\frac{19}{7}-(-3)=\frac{2}{7}

    Тоді значення с буде:

    c=7\cdot\frac{2}{7}\cdot(-3)=-6

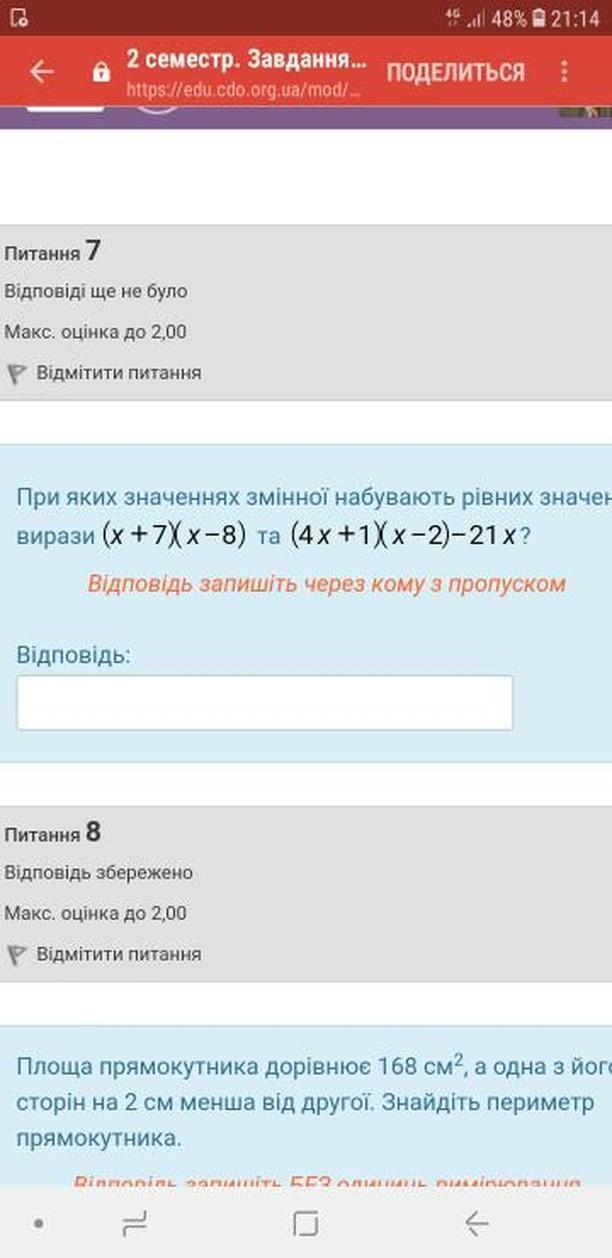
    Питання 7.

    Порібно розв'язати рівняння:

    (x+7)(x-8)=(4x+1)(x-2)-21x;\\x^2+7x-8x-56=4x^2+x-8x-2-21x;\\3x^2-27x+54=0;\\x^2-9x+18=0;\\x_1=3;\,x_2=6.

    (корені знайдені за теоремою Вієта: їх добуток 18, а сума 9)

    Питання 8.

    Якщо позначити меншу сторону прямокутника за x, то за умовою його більша сторона буде дорівнювати x+2 і маємо рівняння:

    x(x+2)=168;\\x^2+2x-168=0;\\D=b^2-4ac=4-4\cdot(-168)=4+672=676=26^2;\\x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-2+26}{2}=12;\\x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-2-26}{2}=-14<0.

    Другий знайдений корінь рівняння не може задовольняти умову задачі, тому сторони прямокутника дорівнюють 12 см і 12+2=14 см, а периметр дорівнює:

    P=(12+14)\cdot2=52 сантиметра.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years