-
Помогите пожалуйста решить эту систему неравенств!!
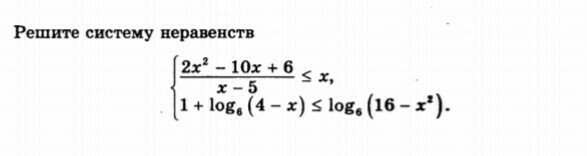
-
Предмет:
Математика -
Автор:
shilohliu - 6 лет назад
-
Ответы 2
Еще вопросы
-
Прошу, молю вас помогите пожалуйста с решением данной задачи...
-
Предмет:
Алгебра -
Автор:
baby cakes - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В данном ниже предложении найди слово в котором все согласные звуки звонкие. У подножия клёнов ковром лежали жёлтые листья
-
Предмет:
Русский язык -
Автор:
deweysantiago - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
автобус подьезжает к остановке. пассажир с ребенком на руках подходит к передней двери. относительно каких тел ребенок находиться в покое?
а)водитель автобуса
б)кондуктора, находящегося на задней площадке автобуса
в)пассажира, у которого он находиться на руках
г)людей на остановке-
Предмет:
Физика -
Автор:
sheahinton - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
ПОМОГИТЕ!!!
ЗАДАНИЕ 8. Прочитайте русские пословицы, поговорки, приметы о гостеприимстве, ответьте на вопросы:
Вопрос 1. При помощи каких средств в слове, обозначающем лицо, выражается грамматическое значение женского рода?
Нож со стола упал - гость будет, ложка или вилка - гостья.
Вопрос 2. С помощью какой морфологической формы выражено противопоставление в данной пословице? Ответ поясните.
На земле гостем жить хорошо, а хозяином лучше того.
Вопрос 3. Какой звук произносится на конце данного слова - "Бог". Ответ поясните.
Гость в дом - Бог в дом.-
Предмет:
Русский язык -
Автор:
midnightqaso - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
