-
Нужно подробное решение этих примеров, желательно на листе.
4. Даны координаты точек
A1, A2, A3, A4.
а) вычислить объём тетраэдра A1 A2 A3 A4;
б) составить уравнение плоскости A1 A2 A3;
в) составить уравнение прямой A3 A4.
5. Назвать и построить кривую.
6. Найти пределы функций, не пользуясь правилом Лопиталя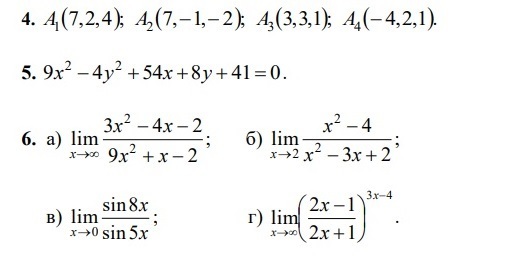
-
Предмет:
Математика -
Автор:
maddievxrc - 6 лет назад
-
Ответы 3
-
Могли бы вы посмотреть остальные мои задачи? (они должны отображаться у меня в профиле)
-
Автор:
ezequielwqme - 6 лет назад
-
0
-
-
Спасибо и с новым годом)
-
Автор:
carlosqxi1 - 6 лет назад
-
0
-
-
4. Даны координаты точек: A1(7; 2; 4), A(7; -1; -2), A3(3; 3; 1), A4(-4; 2; 1).
а) вычислить объём тетраэдра A1 A2 A3 A4.
Находим координаты векторов:
A1 A2 = (0; -3; -6),
A1 A3 = (-4; 1; -3).
A1 A4 = (-11; 0; -3).
Находим векторное произведение (A1 A2) х A1 A3).
Произведение векторов a × b = {aybz - azby; azbx - axbz; axby - aybx} Подставив данные, получаем: x y z
(A1 A2) х A1 A3) = 15 24 -12.
Теперь определяем смешанное произведение векторов:
(A1 A2) х A1 A3) х (A1 A4) = abs(a{x1, y1, z1} ; b{x2, y2, z2} ; c{x3, y3, z3})= x3·a1+y3·a2+z3·a3.
(A1 A2) х A1 A3) х (A1 A4) = |(15*(-11) + (24*0+ (-12)*(-3))| = |-165 + 0 + 36| = 129.
Объём пирамиды равен (1/6)*129 = 21,5 куб.ед.
б) составить уравнение плоскости A1 A2 A3.
Если вектор N(A1 А2) - вектор-нормаль плоскости, а точка M
0(x0; y0; z0) - лежит на плоскости, то уравнение плоскости можно найти по формуле:
A(x − x0) + B(y − y0) + C(z − z0) = 0.
Т.к. векторное произведение - это вектор ортогональный векторам в произведении, то в качестве вектор-нормали плоскости можно взять векторное произведение любых неколлинеарных векторов лежащих на плоскости. Возьмём вектор А1А2, который уже определён.
В качестве точки лежащей на плоскости можно взять любую из трех данных точек. Возьмём точку A1(7; 2; 4).
Подставим в формулу найденные числа и раскроем скобки:
15(x − 7) + 24(y − 2) − 12(z − 4) = 0.
15x + 24y − 12z −105 = 0 или, сократив на 3, получаем:
5x + 8y − 4z − 35 = 0.
в) составить уравнение прямой A3(3; 3; 1), A4(-4; 2; 1).
(x - 3)/(-7) = (y - 3)/(-1) = (z - 1)/0 = 0. Это каноническое уравнение.
Параметрическое уравнение прямой:
x=3-7t
y=3-t
z=1+0t.
5. Назвать и построить кривую: 9x² - 4y² + 54x + 8y + 41 = 0.
Это уравнение гиперболы. Детали и график приведены в приложении.
-
Автор:
raul133 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Вычислите 3xyz-x^3-y^3-z^3,если x=1293 y=715 z=-2008.(если что ^3 означает в 3 степени)
-
Предмет:
Математика -
Автор:
nataly - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
построй прямоугольник периметр которого равен 20 см
-
Предмет:
Математика -
Автор:
calvin365 - 6 лет назад
-
Ответов:
8 -
Смотреть
-
-
Составьте предложения из предложенных в каждой цепочке слов.
1) is, tuition, fee, in, ones, universities, in, much, private, lower, public, than.
2) railway, is, with, transport, construction, our, connected, university, railway, and.
3) of, provide, degrees, Russian, different, universities, education
4) terms, American, goals, do, of, in, universities, vary, how?
5) four, a, be, of, Bachelor, can, years, degree, obtained, studies, after, of.-
Предмет:
Английский язык -
Автор:
potts - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Яка пара чисел є розв'язком рівняння 5х+3у=4
