Задать вопрос Регистрация
Помочь другим

  • а) решите уравнение 1/tg²x -1/sinx=1
    ь) Найдите все корни этого уравнение...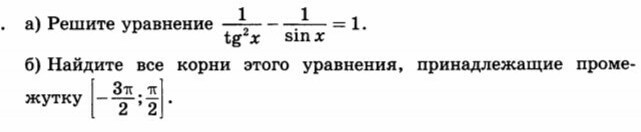

    question img

Ответы 2

  • А) \frac{1}{3g^{2} x} - \frac{1}{sin (x)}

    \frac{sin (x) * 1}{sin (x) * 3g^{2} x} - \frac{3g^{2} x * 1}{3g^{2} x * sin (x)}

    \frac{sin (x)}{3g^{2}x * sin (x) } - \frac{3g^{2} x}{3g^{2} x* sin (x)}

    \frac{sin (x)-3g^{2} x}{3g^{2} x*sin (x)}

    Б) -\frac{3p}{2}  = - \frac{3p}{2} * \frac{180^{0} }{p} = -270^{0};

    \frac{p}{2} =\frac{p}{2} * \frac{180^{0} }{p} = 90^{0}

  • Ответ:

    Пошаговое объяснение:

    sinx≠0, x≠π*n, n∈Z,

    \frac{cos^{2} x}{sin^{2} x} -\frac{1}{sinx} -1=0

    Умножим уравнение на sin^{2} x. Получим:

    cos^{2}x-sinx-sin^{2} x=0

    1-sin^{2} x-sinx-sin^{2} x=0

    -2sin^{2} x-sinx+1=0

    Пусть sinx=y, тогда 2y^{2} +y-1=0

    Уравнение имеет корни y=-1 и y=\frac{1}{2}

    sinx=-1,    x=-\frac{\pi }{2} +2\pi n, где n∈Z

    sinx=\frac{1}{2},   x=(-1)ⁿ\frac{\pi }{6} +\pi n, где n∈Z

    б) отмечая числа на тригонометрическом круге отберем корни принадлежащие промежутку

    -\frac{7\pi }{6} ; -\frac{\pi }{2} ; \frac{\pi x}{6}

    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years