Задать вопрос Регистрация
Помочь другим

  • Решить дифференциальное уравнение (подробнее)
    Пожалуйста, помогите, очень надо.... Плииз)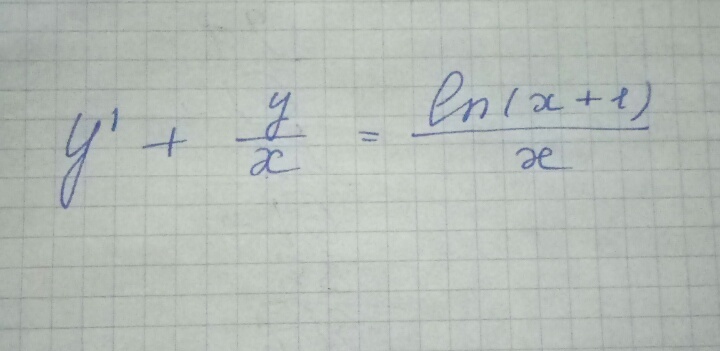

    question img

Ответы 1

  • Ответ:

    \Large \displaystyle y = \ln(1 + x) - 1 + \frac{\ln(1 + x)}{x} + \frac{C_3}{x}

    Пошаговое объяснение:

    y' + \frac{y}{x} = \frac{\ln(1 + x)}{x}\\xy' + y = \ln(1 + x)\\x\frac{dy}{dx} + y = \ln(1 + x)

    По формуле производной произведения:

    xy' + y = (xy)', так как (x)' = 1.

    \frac{d(xy)}{dx} = \ln(1 + x)\\\int {d(xy)} = \int {\ln(1 + x)} \, dx\\xy + C_1= \int {\ln(1 + x)} \, dx

    Интегрируем по частям:

    \int {\ln(1 + x)} \, dx = x\ln(1 + x) - \int {x} \, d(\ln(1 + x)) = x\ln(1 + x) - \int {(1 - \frac{1}{x + 1})} \, dx =\\= x\ln(1 + x) - x + \ln(1 + x) + C_2

    xy = x\ln(1 + x) - x + \ln(1 + x) + C_3\\y = \ln(1 + x) - 1 + \frac{\ln(1 + x)}{x} + \frac{C_3}{x}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years