Найти частное решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Найти частное решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.
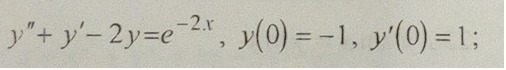
- Предмет:
  Математика
- Автор:
  godivaxejw
- 6 лет назад

Ответы 6

Условие читайте! Найти нужно частное решение а не общее решение неоднородного!
- Автор:
  rosasnu5
- 6 лет назад
- 0
Найти частное решение от общего решения неоднородного уравнения.
- Автор:
  franco
- 6 лет назад
- 0
Ваш вопрос отличается от вопроса задающего! Не стоит себя напрягать с высока
- Автор:
  presley16
- 6 лет назад
- 0
Такие задания задают, если в условии записано ЛНДУ 2-го порядка с постоянными коэффициентами. Просто вопрос до конца полностью не написали... Не было бы смысла в условии задавать лин. неоднор. диффер. ур-ие с пост. коэфф.
- Автор:
  leandrocompton
- 6 лет назад
- 0
хотя я понял что вы имеете ввиду. Нужно было решить задачу Коши)
- Автор:
  snowball
- 6 лет назад
- 0
Найдем сначала общее решение соответствующего однородного уравнения:
$y''+y'-2y=0$
Пусть $y=e^{kx}$ , тогда получаем характеристическое уравнение:
$k^2+k-2=0$
$k_1=-2\\ k_2=1$
Общее решение однородного уравнения: $y^*=C_1e^{-2x}+C_2e^x$
Рассмотрим правую часть $f(x)=e^{-2x}$
Здесь $P_n(x)=1~~\Rightarrow~~~ n=0;~~~ \alpha=-2$ . Сравнивая α с корнями характеристического уравнения и ,принимая во внимая, что n=0 частное решение будем искать в виде:
$\overline{y}=Axe^{-2x}$
Вычислим первую и вторую производные функции
$y'=(Axe^{-2x})'=Ae^{-2x}-2Axe^{-2x}\\ y''=-2Ae^{-2x}-2Ae^{-2x}+4Axe^{-2x}=-4Ae^{-2x}+4Axe^{-2x}$
Подставляем в исходное уравнение
$-4A+4Ax+A-2Ax-2Ax=1\\ -3A=1\\A=-\dfrac{1}{3}$
$\overline{y}=-\dfrac{1}{3}xe^{-2x}$
Общее решение неоднородного уравнения:
$y=y^*+\overline{y}=C_1e^{-2x}+C_2e^x-\dfrac{1}{3}xe^{-2x}\\ \\\\ y'=-2C_1e^{-2x}+C_2e^x+\dfrac{2}{3}xe^{-2x}-\dfrac{1}{3}e^{-2x}$
Найдем частное решение подставив начальные условия
$\displaystyle \left \{ {{-1=C_1+C_2} \atop {1=-2C_1+C_2-\dfrac{1}{3}}} ight. ~~~\Rightarrow~~~\left \{ {{C_1=-\dfrac{7}{9}} \atop {C_2=-\dfrac{2}{9}}} ight.$
Получаем ответ: $y=-\dfrac{7}{9}e^{-2x}-\dfrac{2}{9}e^x-\dfrac{1}{3}xe^{-2x}$
- Автор:
  magnolia
- 6 лет назад
- 0
Добавить свой ответ