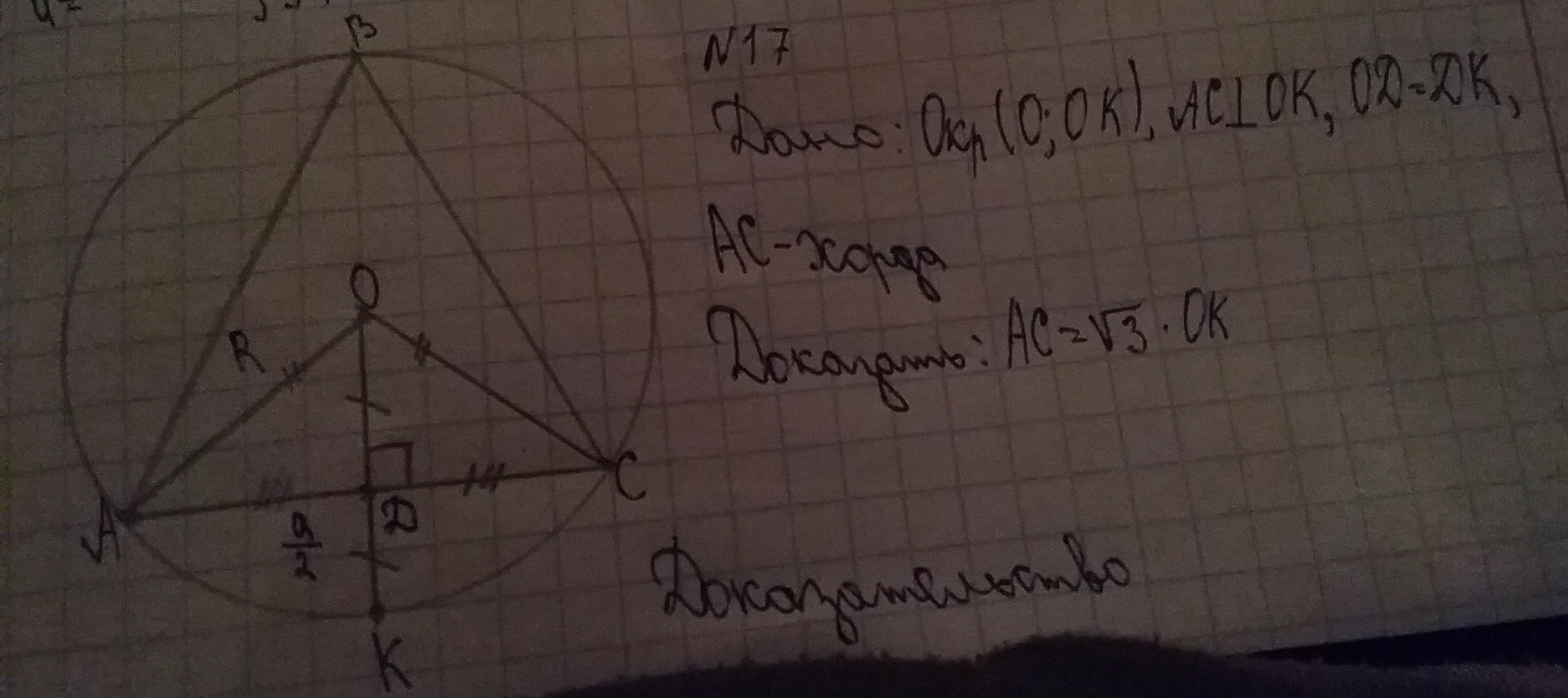
Хорда, перпендикулярная радиусу и проходящая через его середину, равна стороне правильного вписанного треугольника. Докажите.

но,может и правильный мне уже написали ответ.

и ониотличаеться оо этого

И что из этого! Я разве от Вас чего требую? Я в чем-то виновата? Или должна Вам? Мне кажется, я Вам ничего не должна. Могли бы просто написать «спасибо».Существует, по меньшей мере, 3 способа доказательства для Вашей задачи.К тому же у Вас напечатано условие одно, а на прилагаемой картинке другое.А это некорректно, и я могла Ваше задание отметить как нарушение. Вместо этого решила Вам помочь. А Вы обесценили моб работу.

спасибо

) На здоровье!

Рассмотрим треугольник АОД. Он прямоугольный, поскольку хорда АС перпендикулярна радиусу ОК.По условию хорда АС делит радиус ОК пополам. Так что ОД = R/2Но AO = RСледовательно, ОД = АО/2Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то угол, противоположный этому катету, равен 30 градусов.Докажем это.ОД/АО = sin OAДsin ОАД = 1/2<ОАД = 30 градусовЭти же рассуждения верны для треугольника ДОС, следовательно < ОСД=30 градусов.< АОС = 180 - (<ОАД + <ОСД) = 180-(30+30) = 120 градусов.Линия ДВ делит треугольник АВС пополам, так как ОВ общая сторона, АД = ДС, а < АДО = <ОДС = 90 градусов.Можно посчитать чему равен наружный угол АОС:<АОС = 360-120 = 240 градусов.Тогда < АОВ = <ВОС = < АОС/2 = 240/2=120 градусов.Поскольку ОВ = R, то следующие треугольники равны:АОВ = ВОС = АОССЛЕДОВАТЕЛЬНО, равны и соответствующие стороны треугольника АВС:АВ = ВС = САА это значит, что треугольник АВС равносторонний