Задать вопрос Регистрация
Помочь другим

  • Нужно найти производные функций только подробное решение

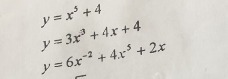
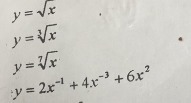
    question img
    question img

Ответы 2

  • y = x {}^{5} + 4 \\ \frac{d}{dx} (x {}^{5} ) + \frac{d}{dx} (4) \\ 5x {}^{4} + 0 = 5x {}^{4} \\ y = 3x {}^{3} + 4x + 4 \\ \frac{d}{dx} (3x {}^{3} ) + \frac{d}{dx} (4x) + \frac{d}{dx} (4) \\ 3 \times 3x {}^{2} + 4 + 0 = 9x {}^{2} + 4 \\ y = 6x {}^{ - 2} + 4x {}^{5} + 2x \\ \frac{d}{dx} (6x {}^{ - 2} ) + \frac{d}{dx} (4x {}^{5} ) + \frac{d}{dx} (2x) \\ 6 \times ( - 2x {}^{ - 3} ) + 4 \times 5x {}^{4} + 2 \\ - \frac{12}{x {}^{3} } + 20x {}^{4} + 2 \\ y = \sqrt{x} = \frac{1}{2 \sqrt{x} } \\ y = \sqrt[3]{x} \\ \frac{d}{dx} (x {}^{ \frac{1}{3} } ) \\ \frac{1}{3} x {}^{ - \frac{2}{3} } = \frac{1}{3 \sqrt[3]{x {}^{2} } } \\ y = \sqrt[7]{x} \\ \frac{d}{dx} (x {}^{ \frac{1}{7} } ) \\ \frac{1}{7} x {}^{ - \frac{6}{7} } \ = \frac{1}{7 \sqrt[7]{x {}^{6} } } \\ y = 2x {}^{ - 1} + 4x {}^{ - 3} + 6x {}^{2} \\ \frac{d}{dx} (2x {}^{ - 1} ) + \frac{d}{dx} (4x {}^{ - 3} ) + \frac{d}{dx} (6x {}^{2} ) \\ 2 \times ( - 1x {}^{ - 2} ) + 4 \times ( - 3x {}^{ - 4} ) + 6 \times 2x \\ - \frac{ - 2x {}^{2} - 12 + 12x {}^{5} }{x {}^{4} }

    • Автор:

      sadie11
    • 5 лет назад
    • 0

  • Ответ:

    Пошаговое объяснение:

    y' = 5x^4+0 = 5x^4\\\\y'=9x^2+4\\\\y'=-12x^{-3}+20x^4+2

    формула:

    (x^n)'=nx^{n-1}

    вторая часть:

    y'=(x^\frac{1}{2} )'=\frac{1}{2} x^{-\frac{1}{2} }=\frac{1}{2\sqrt{x} } \\\\y'=(x^\frac{1}{3} )'=\frac{1}{3} x^{-\frac{2}{3} }=\frac{1}{3\sqrt[3]{x^2} } \\\\y'=(x^\frac{1}{7} )'=\frac{1}{7} x^{-\frac{6}{7} }=\frac{1}{7\sqrt[7]{x^6} } \\\\y'=-2x^{-2}-12x^{-4}+12x

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years