-
определелить для данной функции её основные свойства
применить свойства функции в построение графика
определить точки экстремума,асимптоты,точки перегиба
помтроить график используя свойства функции
ПОЖАЛУЙСТА СРОЧНО ВЫСШАЯ МАТЕМАТИКА .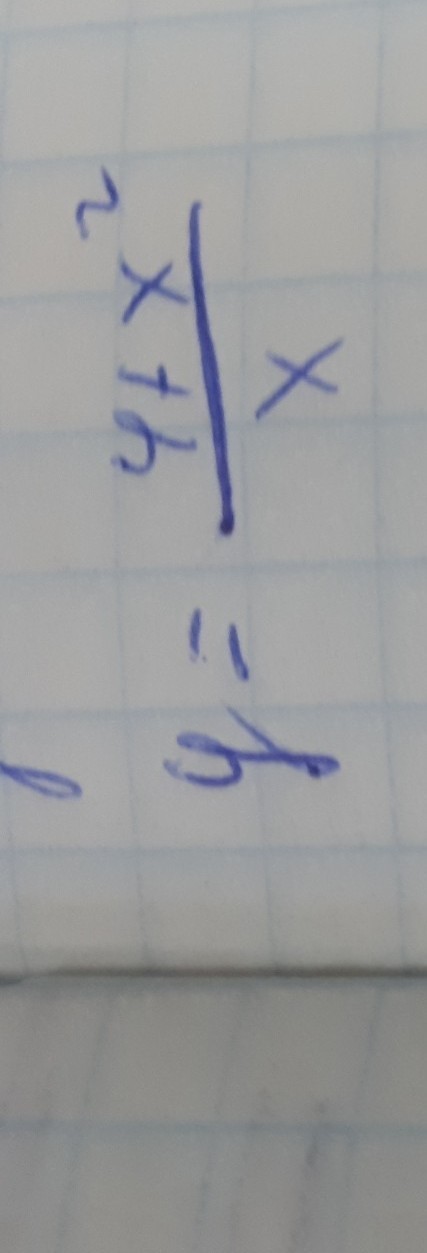
-
Предмет:
Математика -
Автор:
banks - 6 лет назад
-
Ответы 1
-
ДАНО: Y = (x²+4)/x.
ИССЛЕДОВАНИЕ
1. Область определения: D(y)= X≠ 0 , X∈(-∞;0)∪(0;+∞). Не допускаем деления на 0 в знаменателе.
2. Разрыв II-го рода при Х = 0. Вертикальных асимптота - Х =0.
3.Поведение на бесконечности. Y(-∞)= -∞, Y(+∞)= +∞ - горизонтальной асимптоты - нет.
4. Нули функции, пересечение с осью ОХ.
x² = - 4. Корней нет.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;0).
Положительна: Y>0 - X∈(0;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция ни чётная, ни нечётная: Y(-x) ≠ -Y(x) , Y(-x)≠ Y(x).
7. Поиск экстремумов по первой производной.
y'(x) = 1 - 4/x² = 0. x² = 4, x = ±2 - точки экстремумов.
8. Локальный максимум: y(-2) = -4, минимум: y(2) = +4.
9. Интервалы монотонности.
Возрастает - X∈(-∞;-2)∪(2;+∞). Убывает: X∈(-2;0)∪(0;2).
10. Поиск перегибов по второй производной.
y"(x) = 8/x³ = 0
Точки перегиба нет, кроме разрыва при Х = 0.
11. Вогнутая - "ложка"- X∈(0;+∞;), выпуклая - "горка" X∈(-∞;0);
12. Наклонная асимптота.
k = lim(+∞) Y(х)/x = (x²+4)/x² = 1 - наклон. y = x - асимптота.
13. Область значений. E(y) = (-∞;+∞).
14. График функции на рисунке в приложении.

-
Автор:
ash - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Определите частоту, период, угловую скорость и линейную скорость, если за 20 секунд тело совершает 40 оборотов. И дано
-
Предмет:
Физика -
Автор:
turtlelwrj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В корзине 3 красных и 6 белых шаров. Сколько способов вытащить 6 шаров, чтобы хотя бы 1 был красным?
-
Предмет:
Математика -
Автор:
tracker - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Определите число колебаний груза на на пружине за все время, равное 20 с, если частота его колебаний равна 4 Гц
-
Предмет:
Физика -
Автор:
peanutsr8dx - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
две снегоуборочные машины выехали в 8 утра и поехали в одном направлении .в 11 часов расстояние между ними было 6 км.с какой скоростью двигалась одна из машин если скорость другой 30км/ч
-
Предмет:
Математика -
Автор:
hank - 6 лет назад
-
Ответов:
1 -
Смотреть
-
