Задать вопрос Регистрация
Помочь другим

  • Логарифмические уравнения - самое страшное, что я когда-либо видел, просто помогите

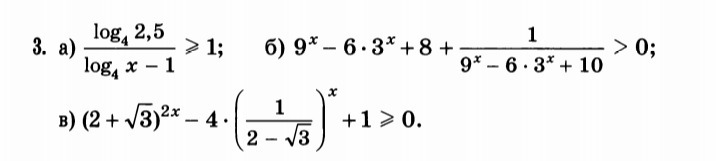
    question img

Ответы 2

  • Добрейший человек, спасибо

    • Автор:

      laramad6
    • 5 лет назад
    • 0

  • Ответ:

    а) (4;5]

    Пошаговое объяснение:

    3.а)

    Приведём к общему знаменателю:

    \frac{\log_{4}{2,5}-\log_{4}{x}+\log_{4}{2,5}+1}{\log_{4}{x}-1}\geq0 \Leftrightarrow \frac{\log_{4}{(\frac{5}{2}\cdot\frac{5}{2})}-\log_{4}{x}+1}{\log_{4}{x}-1}\geq0 \Leftrightarrow \frac{\log_{4}{\frac{5}{4} }-\log_{4}{x}+1}{\log_{4}{x}-1}\geq0 \Leftrightarrow \frac{\log_{4}{5}-\log_{4}{4}-\log_{4}{x}+1}{\log_{4}{x}-1}\geq0 \Leftrightarrow \frac{\log_{4}{x}-\log_{4}{5}}{\log_{4}{x}-1}\leq 0

    Ограничения на логарифмы:

    x>0

    \frac{x-5}{x-4}\leq 0 \Leftrightarrow x \in (4;5]

    Думаю подробно расписал

    P.S. в пункте б) необходимо взять 9^{x}-6\cdot3^{x}+8=y, после чего неравенство приводится к виду y+\frac{1}{y+2}>0

    в пункте в) необходимо решить квадратное неравенство относительно y^2-4y+1\geq0; y=2+\sqrt{3}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years