-
Вычислите и объясните почему детально каждое действие
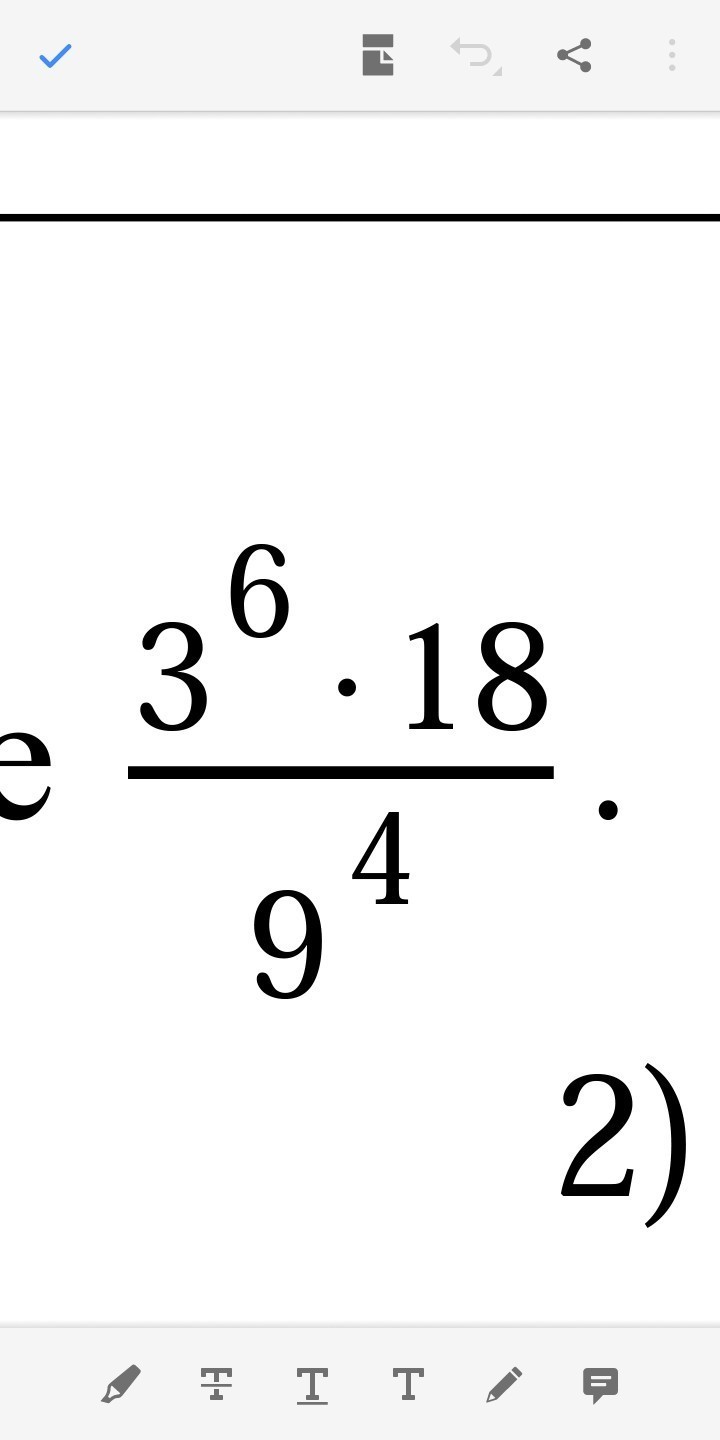
-
Предмет:
Математика -
Автор:
underwood - 6 лет назад
-
Ответы 5
-
Объяснить действия надо
-
Автор:
emmybenitez - 6 лет назад
-
0
-
-
тут по моему все понятно
-
Автор:
gigi43 - 6 лет назад
-
0
-
-
Объяснить по каким пррзнакам сделано действия
-
Автор:
anthony49 - 6 лет назад
-
0
-
-
-
Автор:
cinnamonir7j - 6 лет назад
-
0
-
-
Знак ^ здесь показывает, что после него написан показатель степени.Скобки я использую для того, чтобы выделить числа в степени , числители и знаменатели.Для начала объясню Вам то, что Вы, возможно, уже знаете:9 = 3^2 (3 в квадрате)Тогда 9^4 можно записать как (3^2)^4, то есть 3 в квадрате возводим в четвертую степень.Известно, что при возведении в степень числа, уже возведенного в какую-то степень, основание оставляем без изменения, а показатели степени перемножаем:Тогда:9^4 = (3^2)^4 = 3^8Ещё можно преобразовать число 18:18 = 2 • 9 = 2 • 3^2, то есть 2 умножить на 3 в квадрате.Кроме того, нужно помнить, что при перемножении чисел с одинаковым основанием, возведённых в степень, показатели степени суммируются, а при делении - вычитаются. Например, 3 в квадрате умножить на 3 в кубе:3^2 • 3^3 = 3^(2+3) = 3^5То есть получится 3 в пятой степени.Проверим: 3^2 = 3•33^3 = 3•3•33^2 • 3^3 = 3•3•3•3•3 = 3^5Или 3 в квадрате делим на 3 в кубе:3^2 : 3^3 = 3^(2-3) = 3^(-1) = 1/3Проверим:3^2 / 3^3 = 3•3 / (3•3•3) = 1/3Отрицательный показатель степени показывает, что число, возведённое в степень, оказывается в знаменателе дроби. То есть:5^(-2) = 1/(5^2) (1 находится в числителе, а 5 в квадрате - в знаменателе.А теперь решаем Ваш пример:(3^6 • 18) / 9^4 = = (3^6 • 9 • 2) / ((3^2)^4) == (3^6 • 3^2 • 2) / (3^8) == (3^(6+2) • 2 / (3^8) == (3^8 • 2) / (3^8) = (В числителе и знаменателе сокращаем 3 в восьмой степени. В числителе остается 2)= 2
-
Автор:
kaitlynnsummers - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
20 баллов.
Задача 21,38
Помогите пожалуйста. -
В треугольнике ABC угол C=90°, угол A=30°; AC=34√3. Найдите AB-?
-
Предмет:
Геометрия -
Автор:
baileymorris - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найвище місце в Антарктиді
-
Предмет:
География -
Автор:
mandybooth - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Найти молекулярную формулу предельного одноатомного спирта, если его молекулярная масса равна 37
How much to ban the user?
1 hour
1 day
100 years
