-
ПОМОГИТЕ, ПОЖАЛУЙСТА!
Задание:
1. Для функции y=f(x) найдите:
Производную;
Критические точки;
Промежутки монотонности и экстремумы;
По результатам составьте таблицу.
2. Постройте график функции y=f(x) и y=f`(x) в одной системе координат
3. Напишите уравнение касательной к графику функции, проходящей через х0
4. Вычислите угол наклона касательной к графику функции в точке х0
Буду очень благодарна!!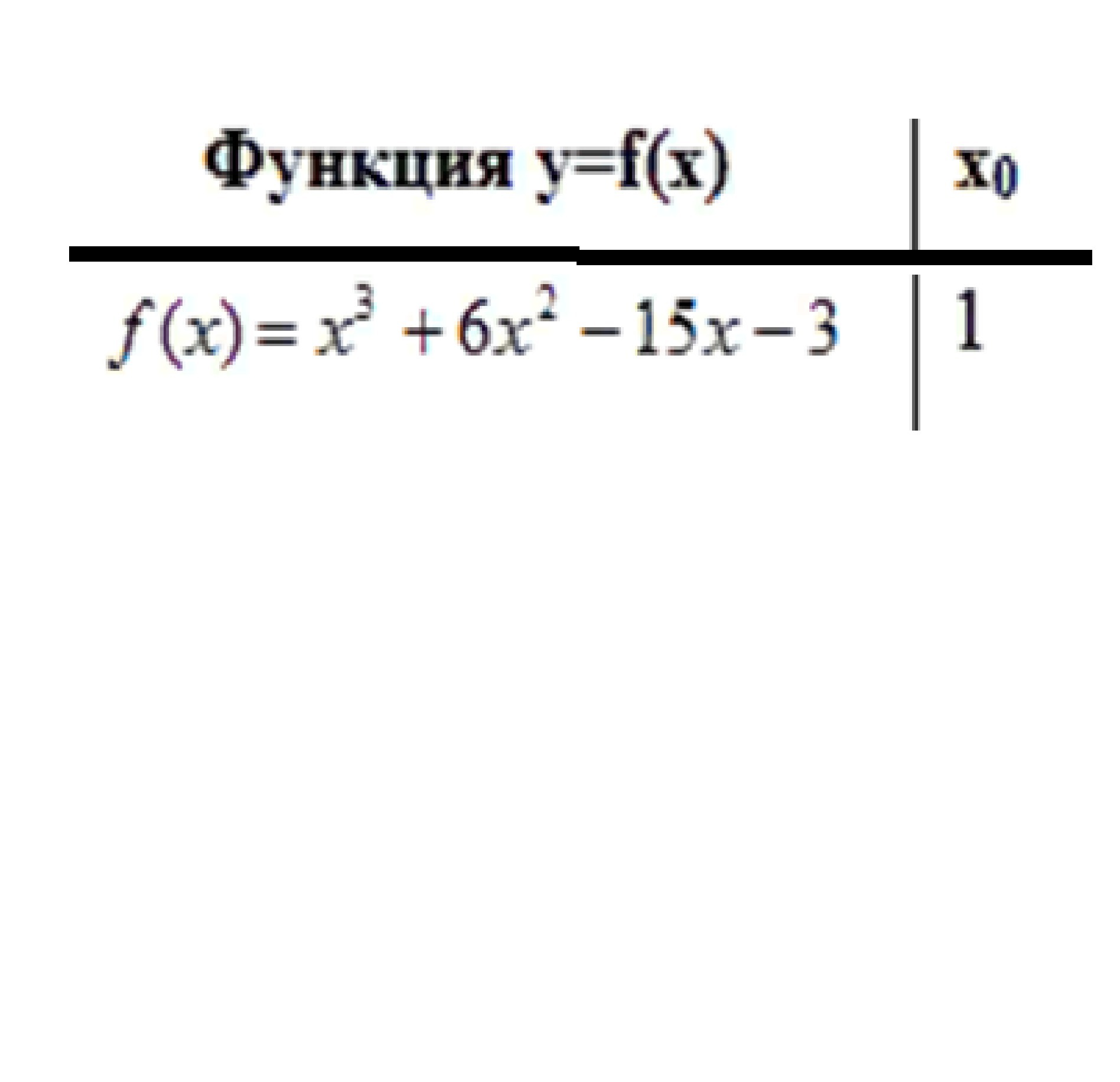
-
Предмет:
Математика -
Автор:
peña61 - 6 лет назад
-
Ответы 2
-
Спасибо большое))
-
Автор:
titan10 - 6 лет назад
-
0
-
-
ДАНО:Y(x) = x³ + 6*x² -15*x -3
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
Применим тригонометрическую формулу Виета.
Разложим многочлен на множители. Y=(x+7,86)*(x+0,19)*(x-2,05)
Нули функции: Х₁ =-7,86, Х₂ =-0,19, Х₃ =2,05
3. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-7,86]U[-0,19;2,05]
Положительная -Y(x)>0 X∈[-7,86;-0,19]U[2,05;+∞)
4. Пересечение с осью OY. Y(0) = -3
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная - функция общего вида.
6. Первая производная. Y'(x) = 3*x² + 12*x -15 = 0
Корни Y'(x)=0. Х4=-5 Х5=1
Положительная парабола - отрицательная между корнями
7. Локальные экстремумы.
Максимум Ymax(X4=-5) =97. Минимум Ymin(X5=1) =-11
8. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-5;]U[1;+∞) , убывает - Х∈[-5;1]
9. Вторая производная - Y"(x) = 6* x + 12 = 0
Корень производной - точка перегиба Х₆=-2
10. Выпуклая “горка» Х∈(-∞; Х₆=-2]
Вогнутая – «ложка» Х∈[Х₆=-2; +∞).
11. График в приложении.
Уравнение касательной.
Уравнение касательной
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 3*x² + 12*х - 15.
Вычисляем в точке Хо = 1.
F'(1) = 0 и F(1) = -11.
Записываем уравнения прямой.
Y(х) = - 11 - касательная - ответ.
Рисунок к задаче в приложении.
Рисунок к задаче в приложении.

-
Автор:
bunnylhja - 6 лет назад
-
0
-
-
Добавить свой ответ
-
В магазин при художественной галерее привезли 287 коробки(-ок) с красками.
Из них 48 — коробки(-ок) с акварелью, что в 2 раза меньше, чем коробок с гуашью, а остальные коробки — с масляными красками.
Сколько коробок с масляными красками привезли в магазин?-
Предмет:
Математика -
Автор:
aurelia - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В каких городах Южной Америки производят изделия из шерсти
-
Предмет:
География -
Автор:
sablestanton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Понидельник начинается в субботу , а восемьдесят три процента дней года начинается с того что
-
Предмет:
Литература -
Автор:
dawsondavidson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Все герои романа Война и Мир.
-
Предмет:
Литература -
Автор:
erin79 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
