-
Найдите интервалы возрастания, убывания и экстремумы функции.
Решите пожалуйста. Если можно подробно.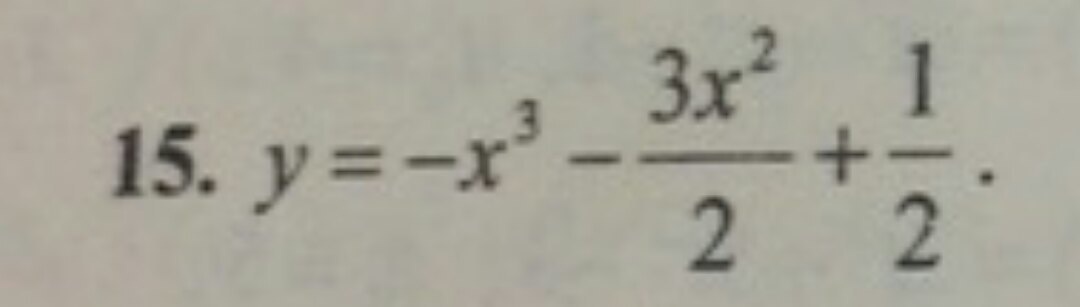
-
Предмет:
Математика -
Автор:
shyannejohns - 6 лет назад
-
Ответы 1
-
ДАНО:Y(x) = -x^3 -1,5*x² + 0,5.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
По теореме Безу - произведение трёх корней равно свободному члену = 0,5. ПРЕДПОЛОЖИМ, что один из корней равен 0,5. Разделим функцию на (x - 0.5)
Разложим многочлен на множители. Y=(x + 1)*(x + 1)*(x-0,5)
Нули функции: Х₁ = -1, Х₂ =-1, Х₃ =0,5
3. Интервалы знакопостоянства.
Положительная - Y(x)>0 X∈(-∞;-1]U[-1;0,5] Отрицательная - Y(x)<0 X∈[-1;-1]U[0,5;+∞)
4. Пересечение с осью OY. Y(0) = 0,5
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная - функция общего вида.
6. Первая производная. Y'(x) = -3*x² -3*x = 0
Корни Y'(x)=0. Х4=0 Х5=-1
7. Локальные экстремумы.
Максимум Ymax(X4=0) =0,5. Минимум Ymin(X5=-1) =0
8. Интервалы возрастания и убывания.
Убывает Х∈(-∞;0;]U[-1;+∞) ,возрастает - Х∈[0;-1]
9. Вторая производная - Y"(x) = -6* x -3 = 0
Корень производной - точка перегиба Х₆= -0,5
10. Выпуклая “горка» Х∈(-∞; Х₆=-0,5]
Вогнутая – «ложка» Х∈[Х₆=-0,5; +∞).
11. График в приложении.

-
Автор:
rosietoql - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Какой второстепенный член с вопросом (в чём?)
-
Предмет:
Русский язык -
Автор:
victoralexander - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Найдите периметр квадрата площадь которого равна площади прямоугольника со сторонами 8см и 18см
-
Предмет:
Математика -
Автор:
penelope - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО
Составьте и оформите пригласительный билет на матч вашего регионального футбольного клуба -
Предмет:
Русский язык -
Автор:
javierjensen - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите тренажёр сложение целых чисел
-
Предмет:
Математика -
Автор:
giovanny - 6 лет назад
-
Ответов:
2 -
Смотреть
-
