-
ПОМОГИТЕ СДЕЛАТЬ ЗАДАНИЕ СОГЛАСНО СХЕМЕ ИССЛЕДОВАНИЯ ФУНКЦИИ
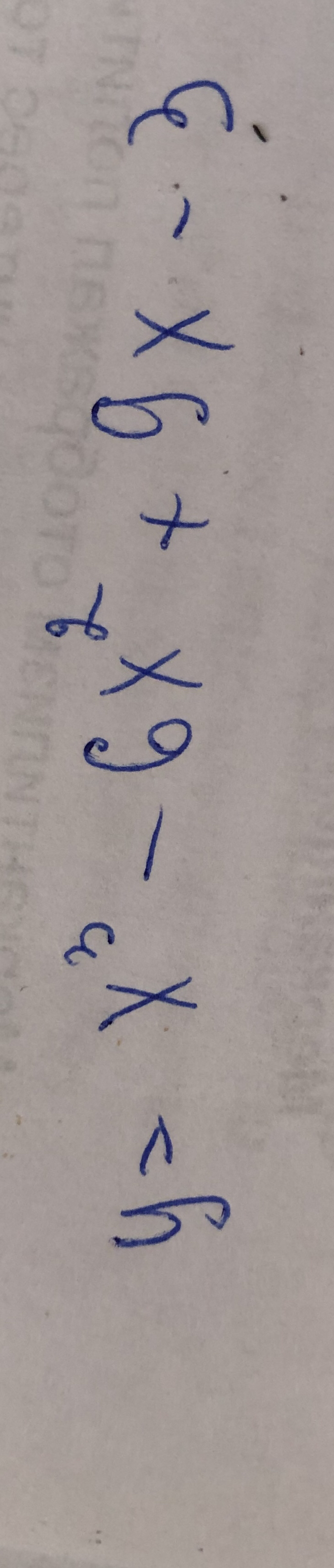

-
Предмет:
Математика -
Автор:
ringo8qfc - 6 лет назад
-
Ответы 6
-
Асимптот просто НЕТ. Нет вертикальных- разрывов, нет наклонных. А уж ход расписан по строчкам.
-
Автор:
scoobiewhitney - 6 лет назад
-
0
-
-
мы так не записываем я создала новое задание и там дан образец как записывать надо
-
Автор:
madisyn - 6 лет назад
-
0
-
-
Нет уж, голубушка! Это ты моё решение запиши, как нужно для записи в тетради. Здесь не так легко писать дроби, дифференциалы, интегралы, А задание посмотрю.
-
Автор:
casperbjfn - 6 лет назад
-
0
-
-
Все пункты уже сделаны - и нули и экстремумы и перегибы
-
Автор:
big nastyshyo - 6 лет назад
-
0
-
-
поэтому задание и не полное
-
Автор:
byron - 6 лет назад
-
0
-
-
ДАНО: y(x) = x^3 -6*x² + 9*x -3.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
Используем теорему Виета.
Разложим многочлен на множители. Y=(x-0,47)*(x-1,65)*(x-3,88)
Нули функции: Х₁ =0,47, Х₂ =1,65, Х₃ =3,88
3. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;0,47]U[1,65;3,88] Положительная -Y(x)>0 X∈[0,47;1,65]U[3,88;+∞)
4. Пересечение с осью OY. Y(0) = -3
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная - общего вида.
6. Первая производная. Y'(x) = 3*x² -12*x + 9 = 0
Корни Y'(x)=0. Х4=1 Х5=3
Положительная парабола - отрицательная между корнями
7. Локальные экстремумы.
Максимум Ymax(X4=1) =1. Минимум Ymin(X5=3) =-3
8. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;1;]U[3;+∞) , убывает - Х∈[1;3]
9. Вторая производная - Y"(x) = 6* x -12 = 0
Корень производной - точка перегиба Х₆=2
10. Выпуклая “горка» Х∈(-∞; Х₆=2]
Вогнутая – «ложка» Х∈[Х₆=2; +∞).
11. График в приложении.

-
Автор:
kelsey - 6 лет назад
-
0
-
-
Добавить свой ответ
- этот архитектурный стиль получивший широкую популярность в Англии 18 века был назван в честь известного итальянского архитектора.
-
Помогите пожалуйста с английским языком.Дам больше баллов.
-
Предмет:
Английский язык -
Автор:
chief - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Последняя по времени основания британская колония в Америке получила свое название в честь короля .
A) Якова II
B) Эдуарда c) Георга l
D)Георга ll
-
Предмет:
Другие предметы -
Автор:
kosmo9fpt - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
найти приблеженно: 25% от 199; 10% от 5045 кг; 24% от 600 р ПОМОГИТЕ ПОЖАЛУЙСТА)
-
Предмет:
Математика -
Автор:
cassiemduz - 6 лет назад
-
Ответов:
1 -
Смотреть
-
