-
Найти частные производные второго порядка u=x*ln*(y+z)
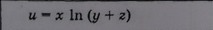
-
Предмет:
Математика -
Автор:
buddy73 - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
-
Автор:
madalynnarwr - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
яке з речень є з послідовною підрядністю ?
а) Коли набираються стяги епохи і вітру нового і висоти дуиай що світ змінити хоч трохи і ти .
б) Слово мама росте разом з нами тихо як тихо ростуть дерева як сходить сонце як тихо світить веселка .
в) Не поет хто покидає боронить народну справу щоб своїм словам близкучим золотую дать оправу-
Предмет:
Українська мова -
Автор:
jakobhnb4 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
построить график функции y=(x+1)^2-1
-
Предмет:
Алгебра -
Автор:
félixspencer - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Почему поход Александра Македонского на саков потерпел положения
-
lim 5x-x^2-4/x^2-2x-8 xстремится к 4
-
Предмет:
Математика -
Автор:
sophiebright - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
