-
Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.
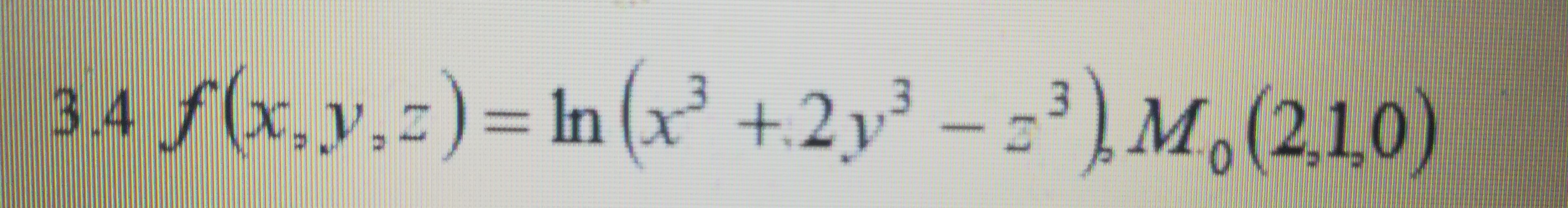
-
Предмет:
Математика -
Автор:
adyson - 6 лет назад
-
Ответы 1
-
-
Автор:
mariyah4iet - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Заполните таблицу:1)причины великих географических открытий
2)Великие географические открытия (первооткрыватель,какие земли открыл)
3)Последствия Великих географических открытий-
Предмет:
История -
Автор:
coconutwelch - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Дам 30 баллов. Пожалуйста можете составить сочинение на тему моя будущая профессия. Английский язык 100-120 слов. Профессия какая вам по душе, но не дворник и т.д. это не канает
-
Предмет:
Английский язык -
Автор:
connornguyen - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Точки M i N лежать на одній із граней двогранного кута і віддалені на 4 см і 5 см відповідно від другої грані. Знайдіть міру двогранного кута, якщо відстань від точки М до ребра двогранного кута 2 си менша, ніж відстань від точки N до реюг двогранного кута
-
Найдите значение выражения: 0,875a-0,39a-0,205a-0,58
При a =4,5-
Предмет:
Математика -
Автор:
ashlynndelgado - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
