-
Найдите точку минимума функции
Часть 2
С 1 Решите уравнение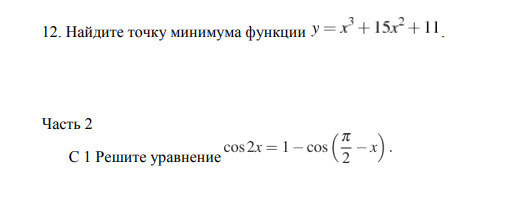
-
Предмет:
Математика -
Автор:
lucas - 6 лет назад
-
Ответы 1
-
Ответ:
Пошаговое объяснение:
12. у=х³+15х²+4
Чтобы найти экстремумы функции, продифференцируем:
у'=3х²+30х и приравняем производную 0:
3х²+30х=0 => х(х+10)=0 =>
х1=0; х2=-10
Рассмотрим интервалы
х<-10
-10<х<0
х>0
Определим интервалы возрастания и убывания функции
у' (-11)=363-330=33>0, значит в интервале
х<-10 функция возрастает.
у'(-9)=243-270=-27<0, значит в интервале
-10<х<0 функция убывает.
у'(1)=3+30=33>0, значит в интервале
х>0 функция возрастает.
Таким образом минимум функции находится в точке (0; 4)
Часть 2
cos2x=1-cos(п/2 - х)
cos2x=1-2sin²x
cos(п/2 - х) =cosп/2 cosx-sinп/2 sinx=
=-sinx
Тогда получаем уравнение:
1-2sin²=-sinx => 2sin²x-sinx-1=0
Решаем:
sinx=[1+-√(1+8)]/4=(1+-3)/4
sinx1=(1+3)/4=1 => x1=п/2+-2пn
sinx2=(1-3)/4=-1/2 => x2=-п/6+-2пn
где n=0; +-1; +-2; +-3...,
a п - это число пи
-
Автор:
norah - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Скажите пожалуйста какой вывод написать в эссе о насекомых.СРОЧНО
-
Предмет:
Английский язык -
Автор:
destiny - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
2+2*2=? В троичной системе счисления
-
Предмет:
Информатика -
Автор:
amaroallen - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
ДАЮ 40 БАЛОВ. Сьогодні слова пані та пан утверджуються в статусі шанобливих назв, поширюються в діловому й побутовомуспілкуванні , стають звичними у звертаннях.Знайдіть варіант, у якому слово пані та пан ужито недоречно,
a)Шановні пані та панове,
б)вельмишановний пане Іване,
в)Прошу пані,
г)Пані Ковальчук,
д) Пані Ганно Микитівно.
Заранее спасибо!
-
Предмет:
Українська мова -
Автор:
aubriebxhz - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
даю 20 балов. Установіть відповідність між художнім засобом та його назвою
1.«шаблю гостру довгу» А метафора 2. «вся Україна плаче» Б гіпербола 3.«панів повні шанці» В епітет 4.«а мене, Кармалюка, як звірюку гонять» Г порівняння
-
Предмет:
Українська мова -
Автор:
jamierlqt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
