-
Помогите, пожалуйста. Очень нужно.Исследовать методами дифференциального исчисления функцию и построить ее график
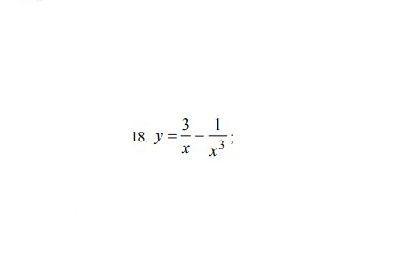
-
Предмет:
Математика -
Автор:
mya - 6 лет назад
-
Ответы 1
-
Дана функция
Провести полное исследование функций по схеме:
1. Область определения функции. Так как переменная в знаменателе, то из области определения выпадает значение х = 0. х ∈ (-∞; 0) ∪ (0; +∞).
2. Непрерывность функции, вертикальные асимптоты. По пункту 1 определяем, что функция имеет разрыв в точке х = 0. Ось Оу - вертикальная асимптота.
3. Точки пересечения функции с осями координат. Так как х не равен нулю, то график функции не пересекает ось Оу.
Для определения точек пересечения оси Ох приравняем функцию нулю. Уравнение приведём к общему знаменателю.
у = (3х² - 1)/х³ = 0. Достаточно приравнять числитель:
3х² - 1 = 0, х = +-√(1/3) ≈ +-0,57735.
4. Четность, нечетность.
f(-x) = (3x² - 1)/(-x³) = -f(x). Функция нечётная.
5. Периодичность - непериодичная.
6. Промежутки возрастания, убывания, экстремумы функции.
Находим производную: y' = (3 - 3х²)/х⁴.
Приравниваем нулю (достаточно числитель):
3 - 3х² = 3(1 - х²) = 0.
Отсюда находим 2 критические точки: х =+-1.
Находим знаки производной в промежутках между критическими точками с учётом точки разрыва х = 0.
х = -2 -1 -0,5 0 0,5 1 2
y' = -0,5625 0 36 - 36 0 -0,5625.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
• Минимум функции в точке: х = -1,
• Максимум функции в точке: х = 1.
• Возрастает на промежутках: (-1; 0) U (0; 1)
• Убывает на промежутках: (-∞; -1) U (1; +∞).
7. Промежутки выпуклости, вогнутости, точки перегиба.
Вторая производная y'' = 6(x² - 2)/x^5. Приравниваем её нулю.
x² - 2 =0. Получаем 2 точки перегиба: х =+-√2 ≈ +-1,4142.
Находим знаки второй производной с учётом точки разрыва х = 0:
х = -2 -√2 -1 1 √2 2
y'' = -0,375 0 6 -6 0 0,375
Интервалы, где функция выпуклая или вогнутая, находим по знаку второй производной : где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
• Вогнутая на промежутках: (-√2; 0) ∪ (√2; +∞),
• Выпуклая на промежутках: (-∞;-√2) ∪ (0; √2) .
8. Наклонные асимптоты - нет, горизонтальная асимптота - ось Ох.
9. Построение графика y(x)=(3/x) − (1/x³) - таблица точек:
x y
-3.0 -0.963
-2.5 -1.136
-2.0 -1.375
-1.5 -1.704
-1.0 -2
-0.5 2
0 -
0.5 -2
1.0 2
1.5 1.704
2.0 1.375
2.5 1.136
3.0 0.963

-
Автор:
greysonzyxr - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Даю 10 баллов.
Определите валентность элементов по формулам; HgO,ZnO,NiO,BaO, PH3, H2O, CH4, HF, HBr-
Предмет:
Химия -
Автор:
jairocollier - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Поймали громадную, давно ослепщую щуку почему, не смотря на слепоту, она упитанная?
-
Предмет:
Биология -
Автор:
patiencemiddleton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
10прилагательных и существетелный слов
-
Предмет:
Русский язык -
Автор:
niko - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
x²+2x-14=7x
Пожалуйста помогите!!!
