-
))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
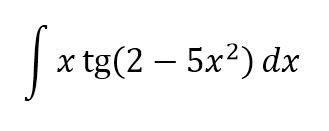
-
Предмет:
Математика -
Автор:
morganhurst - 6 лет назад
-
Ответы 1
-
Ответ:
(1/10)ln|cos(2-5x^2)|+C
x^2=t 2xdx=dt
тогда интеграл примет вид 1/2Int(tg(2-5t)dt=1/2Int(sin(2-5t)/cos(2-5t))dt
вспомним, что (cost)'=-sin(t)
=1/2ln|cos(2-5t)|*1/5=(1/10)ln|cos(2-5t)|+C
возвращаемся к старой переменной
=
Пошаговое объяснение:
x^2=t 2xdx=dt
тогда интеграл примет вид 1/2Int(tg(2-5t)dt=1/2Int(sin(2-5t)/cos(2-5t))dt
вспомним, что (cost)'=-sin(t)
=1/2ln|cos(2-5t)|*1/5=(1/10)ln|cos(2-5t)|+C
возвращаемся к старой переменной
=(1/10)ln|cos(2-5x^2)|+C
-
Автор:
aarónsmith - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
25 баллов!!! помогите пожалуйста
CaCo3+2HCl=CaCl2+H2O+CO2
Рассчитай массу и объем co2 который образуется из 200 г caco3-
Предмет:
Химия -
Автор:
ramóncummings - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
у дитячому садку 14дівчат і 12 хлопців половина дітей пішла гуляти на прогулянку яка найменша кількість дівчат може бути серед них.
А-5 Б-4 В-3 Г -2 Д-1-
Предмет:
Математика -
Автор:
romeobo3p - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
У меня завтра важный экзамен. Как думаете, если я с вечера выпью успокоительное, это никак не повлияет на сдачу завтра?
-
Предмет:
Другие предметы -
Автор:
dearestkver - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- доказать, что если n - простое число и n>3 (n^2-1) делится на 12 нацело
How much to ban the user?
1 hour
1 day
100 years
