Задать вопрос Регистрация
Помочь другим

  • Математики,які ще не сплять. Допоможіть!
    Обчисліть похідні за допомогою логарифмічного диференціювання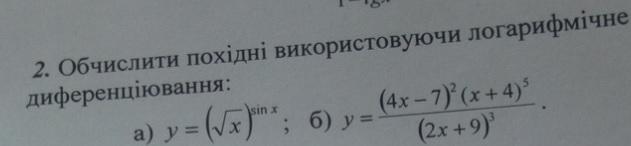

    question img

Ответы 2

  • Дякую ви просто були моя надія!!!!!Спасибі ВАММММ!!!!!!

  • a)

    \(y=(\sqrt{x})^{sinx}\)

    \(lny=ln(\sqrt{x})^{sinx}\)

    \(lny=0,5sinxlnx\)

    \((lny)'=(0,5sinxlnx)'\)

    \(\frac{y'}{y}=0,5cosxlnx+0,5sinx\frac{1}{x}\)

    \(\frac{y'}{y}=0,5cosxln\sqrt{x}+\frac{sinx}{2x}\)

    \(y'=y(0,5cosxln\sqrt{x}+\frac{sinx}{2x})\)

    \(y'=(\sqrt{x})^{sinx}(0,5cosxln\sqrt{x}+\frac{sinx}{2x})\)

    б)

    \(y=\frac{(4x-7)^2(x+4)^5}{(2x+9)^3}\)

    \(lny=ln\frac{(4x-7)^2(x+4)^5}{(2x+9)^3}\)

    \(lny=ln(4x-7)^2+ln(x+4)^5-ln(2x+9)^3\)

    \(\frac{y'}{y}=(ln(4x-7)^2+ln(x+4)^5-ln(2x+9)^3)'\)

    \(\frac{y'}{y}=(2ln(4x-7)+5ln(x+4)-3ln(2x+9))'\)

    \(\frac{y'}{y}=2\frac{4}{4x-7}+5\frac{1}{x+4}-3\frac{2}{2x+9}\)

    \(\frac{y'}{y}=\frac{8}{4x-7}+\frac{5}{x+4}-\frac{6}{2x+9}\)

    \(y'=y(\frac{8}{4x-7}+\frac{5}{x+4}-\frac{6}{2x+9})\)

    \(y'=\frac{(4x-7)^2(x+4)^5}{(2x+9)^3}(\frac{8}{4x-7}+\frac{5}{x+4}-\frac{6}{2x+9})\)

    • Автор:

      rocha
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years