Задать вопрос Регистрация
Помочь другим

  • для умных. Рассмотрим задачку из реального егэ - досрочный егэ 2019, номер 16 пункт Б.
    Краткое условие: абсд трапеция. Через точки б и с проведенна окружность так, что пересекает стороны аб и сд в точка P и Q. Угол CPD прямой. MN - средняя линия, а точки P и Q лежат на отрезках MB и CN. Еще даны все стороны трапеции
    Аб=21,бс=4,сд=20,ад=17. Найти длину отрезка QN.

    Теперь нюанс - получилось доказать, что угол АБС прямой, но вот проблема, сторона АБ больше СД, тогда такой трапеции не существует.
    В комментарии вопросы по доказательству, не получилось добавить полную фотографию доказательства​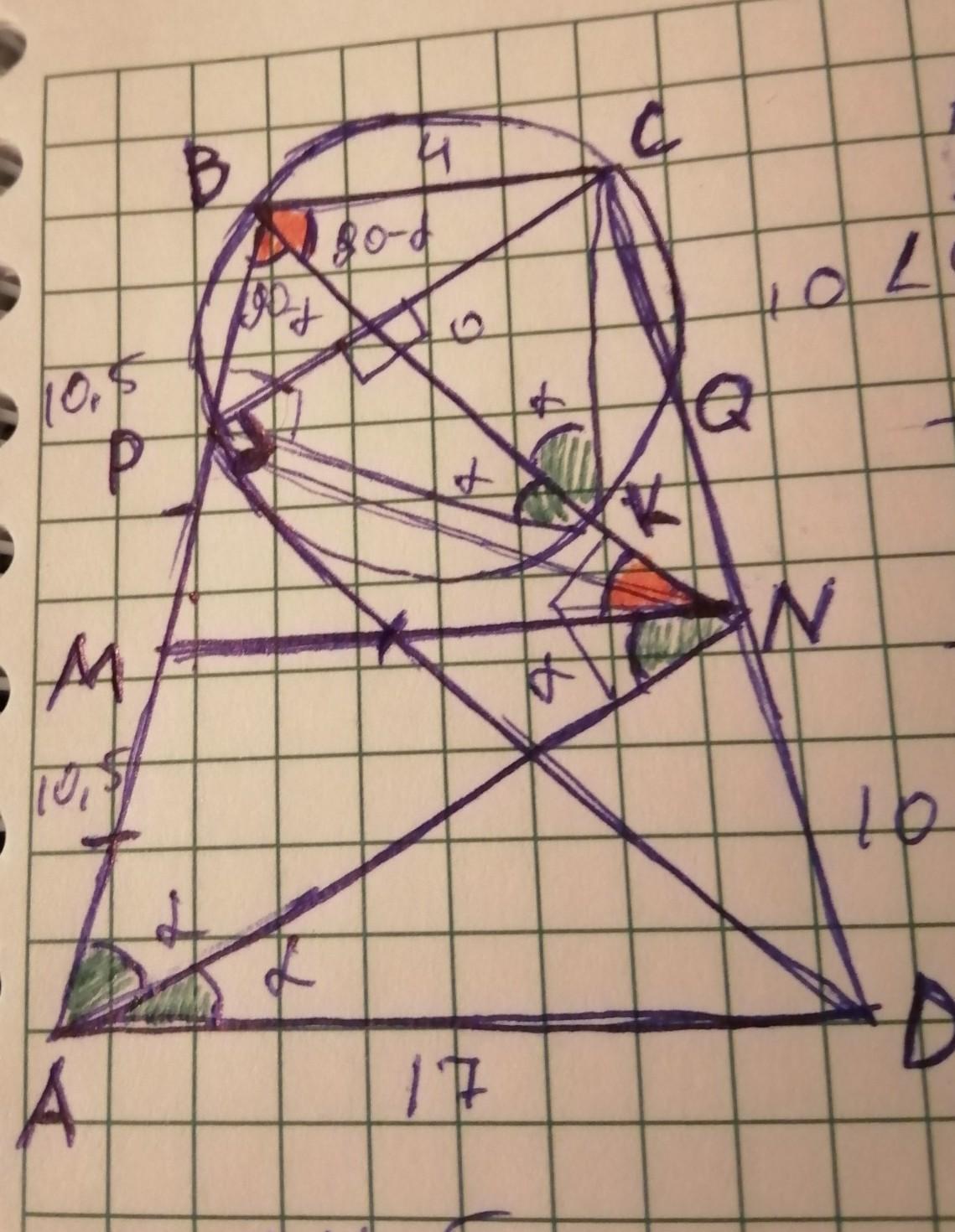

    question img

Ответы 6

  • Но этого мало. Надо определить QN.

    • Автор:

      omary6jr
    • 6 лет назад
    • 0
  • Есть ещё один способ решения - с применением аналитической геометрии. Но он очень громоздкий.

    • Автор:

      marley41
    • 6 лет назад
    • 0
  • по теореме о двух секуших и подобных треугодьнках дальше легко сделать

    • Автор:

      mccarty
    • 6 лет назад
    • 0
  • достроить до треуголька, найти те стороны и воспользоваться теоремой о двух секущих

    • Автор:

      amber16
    • 6 лет назад
    • 0
  • Да, это верный путь к решению.

  • Ответ: длина отрезка QN равна 314/65.  

    Пошаговое объяснение приведено в приложении.

    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years