-
развязать интеграл (определения(визначення) интеграла)ОТ РУКИ НА ЛИСТКЕ
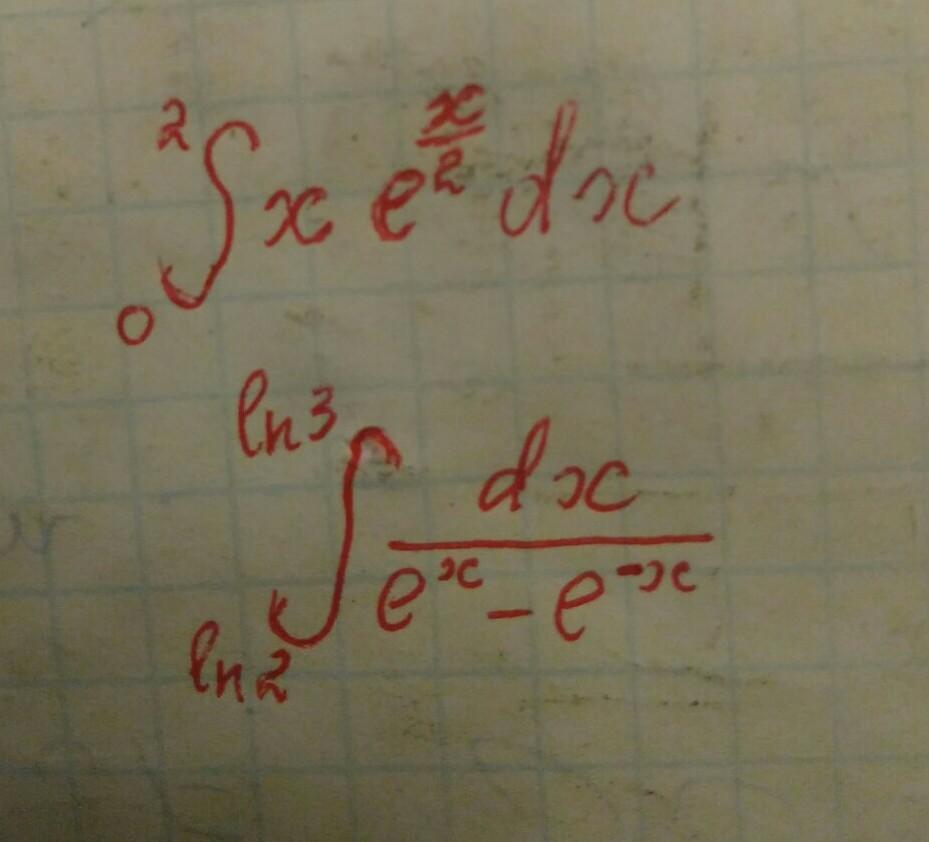
-
Предмет:
Математика -
Автор:
khan - 6 лет назад
-
Ответы 1
-
-
Автор:
amazon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
накресли прямокутник, довжина якого 5см, а ширина у двічі менша. Визнач площу прямокутника
Помогите плиз-
Предмет:
Математика -
Автор:
devanpvpc - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите решить пожалуйста ! Здесь-только нужно true or false! Даю 35 балов!
-
Предмет:
Английский язык -
Автор:
genevieve - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Определите объём водорода, который выделяется при взаимодействии 0,5 моль цинка с необходимым количеством хлоридной кислоты
-
развязать интеграл (определения(визначення) интеграла)ОТ РУКИ НА ЛИСТКЕ
-
Предмет:
Математика -
Автор:
lanesutton - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
